MATHEMATICS
FOR
THE PRACTICAL MAN
EXPLAINING SIMPLY AND QUICKLY
ALL THE ELEMENTS OF
ALGEBRA, GEOMETRY, TRIGONOMETRY,
LOGARITHMS, COÖRDINATE
GEOMETRY, CALCULUS
WITH ANSWERS TO PROBLEMS
BY
GEORGE HOWE, M.E.
ILLUSTRATED
ELEVENTH THOUSAND

NEW YORK
D. VAN NOSTRAND COMPANY
25 Park Place
1918
Copyright, 1911, by
D. VAN NOSTRAND COMPANY
Copyright, 1915, by
D. VAN NOSTRAND COMPANY
𝔖𝔱𝔞𝔫𝔥𝔬𝔭𝔢 𝔓𝔯𝔢𝔰𝔰
F. H. GILSON COMPANY
BOSTON. U.S.A.
Dedicated To
𝔅𝔯𝔬𝔴𝔫 𝔄𝔶𝔯𝔢𝔰, 𝔓𝔥.𝔇.
PRESIDENT OF THE UNIVERSITY OF TENNESSEE
“MY GOOD FRIEND AND GUIDE.”
PREFACE
In preparing this work the author has been prompted
by many reasons, the most important of which are:
The dearth of short but complete books covering the
fundamentals of mathematics.
The tendency of those elementary books which “begin
at the beginning” to treat the subject in a popular rather
than in a scientific manner.
Those who have had experience in lecturing to large
bodies of men in night classes know that they are composed
partly of practical engineers who have had considerable
experience in the operation of machinery, but no
scientific training whatsoever; partly of men who have devoted
some time to study through correspondence schools
and similar methods of instruction; partly of men who
have had a good education in some non-technical field of
work but, feeling a distinct calling to the engineering
profession, have sought special training from night lecture
courses; partly of commercial engineering salesmen, whose
preparation has been non-technical and who realize in this
fact a serious handicap whenever an important sale is to
be negotiated and they are brought into competition with
the skill of trained engineers; and finally, of young men
leaving high schools and academies anxious to become
engineers but who are unable to attend college for that
purpose. Therefore it is apparent that with this wide
difference in the degree of preparation of its students any
course of study must begin with studies which are quite
familiar to a large number but which have been forgotten
or perhaps never undertaken by a large number of others.
iv
v
1
CHAPTER I
And here lies the best hope of this textbook. “It begins
at the beginning,” assumes no mathematical knowledge beyond
arithmetic on the part of the student, has endeavored
to gather together in a concise and simple yet accurate and
scientific form those fundamental notions of mathematics
without which any studies in engineering are impossible,
omitting the usual diffuseness of elementary works, and
making no pretense at elaborate demonstrations, believing
that where there is much chaff the seed is easily lost.
I have therefore made it the policy of this book that
no technical difficulties will be waived, no obstacles circumscribed
in the pursuit of any theory or any conception.
Straightforward discussion has been adopted; where
obstacles have been met, an attempt has been made to
strike at their very roots, and proceed no further until
they have been thoroughly unearthed.
With this introduction, I beg to submit this modest
attempt to the engineering world, being amply repaid if,
even in a small way, it may advance the general knowledge
of mathematics.
GEORGE HOWE.
New York, September, 1910.
TABLE OF CONTENTS
| Chapter | Page | |
|---|---|---|
| I. | Fundamentals of Algebra. Addition and Subtraction | 1 |
| II. | Fundamentals of Algebra. Multiplication and Division, I | 7 |
| III. | Fundamentals of Algebra. Multiplication and Division, II | 12 |
| IV. | Fundamentals of Algebra. Factoring | 21 |
| V. | Fundamentals of Algebra. Involution and Evolution | 25 |
| VI. | Fundamentals of Algebra. Simple Equations | 29 |
| VII. | Fundamentals of Algebra. Simultaneous Equations | 41 |
| VIII. | Fundamentals of Algebra. Quadratic Equations | 48 |
| IX. | Fundamentals of Algebra. Variation | 55 |
| X. | Some Elements of Geometry | 61 |
| XI. | Elementary Principles of Trigonometry | 75 |
| XII. | Logarithms | 85 |
| XIII. | Elementary Principles of Coördinate Geometry | 95 |
| XIV. | Elementary Principles of the Calculus | 110 |
Mathematics
CHAPTER I
Fundamentals of Algebra
Addition and Subtraction
As an introduction to this chapter on the fundamental
principles of algebra, I will say that it is absolutely
essential to an understanding of engineering that the
fundamental principles of algebra be thoroughly digested
and redigested,—in short, literally soaked into one’s
mind and method of thought.
Algebra is a very simple science—extremely simple
if looked at from a common-sense standpoint. If not
seen thus, it can be made most intricate and, in fact,
incomprehensible. It is arithmetic simplified,—a short
cut to arithmetic. In arithmetic we would say, if one
hat costs 5 cents, 10 hats cost 50 cents. In algebra
we would say, if one \(a\) costs 5 cents, then 10 \(a\) cost 50
cents, \(a\) being used here to represent “hat.” \(a\) is what
we term in algebra a symbol, and all quantities are
handled by means of such symbols. \(a\) is presumed
to represent one thing; \(b\), another symbol, is presumed
to represent another thing, \(c\) another, \(d\) another, and
so on for any number of objects. The usefulness
and simplicity, therefore, of using symbols to represent
objects is obvious. Suppose a merchant in the
furniture business to be taking stock. He would go
through his stock rooms and, seeing 10 chairs, he
would actually write down “10 chairs”; 5 tables, he
would actually write out “5 tables”; 4 beds, he would
actually write this out, and so on. Now, if he had at
the start agreed to represent chairs by the letter \(a\),
tables by the letter \(b\), beds by the letter \(c\), and so on,
he would have been saved the necessity of writing
down the names of these articles each time, and could
have written \(10 a\), \(5 b\), and \(4 c\).
2
Definition of a Symbol. — A symbol is some letter by
which it is agreed to represent some object or thing.
When a problem is to be worked in algebra, the first
thing necessary is to make a choice of symbols, namely,
to assign certain letters to each of the different objects
concerned with the problem,—in other words, to get
up a code. When this code is once established it must
be rigorously maintained; that is, if, in the solution of
any problem or set of problems, it is once stipulated
that \(a\) shall represent a chair, then wherever a appears
it means a chair, and wherever the word chair would
be inserted an \(a\) must be placed—the code must not
be changed.
3
Positivity and Negativity. — Now, in algebraic thought,
not only do we use symbols to represent various objects
and things, but we use the signs plus (+) or minus (−)
before the symbols, to indicate what we call the positivity
or negativity of the object.
Addition and Subtraction. — Algebraically, if, in going
over his stock and accounts, a merchant finds that
he has 4 tables in stock, and on glancing over his
books finds that he owes 3 tables, he would represent
the 4 tables in stock by such a form as \(+4a\), \(a\)
representing table; the 3 tables which he owes he would
represent by \(−3a\), the plus sign indicating that which
he has on hand and the minus sign that which he owes.
Grouping the quantities \(+4a\) and \(−3a\) together,
in other words, striking a balance, one would get \(+a\),
which represents the one table which he owns over and
above that which he owes. The plus sign, then, is taken
to indicate all things on hand, all quantities greater
than zero. The minus sign is taken to indicate all
those things which are owed, all things less than zero.
4
Suppose the following to be the inventory of a certain
quantity of stock: \(+8a\), \(−2a\), \(+6b\), \(−3c\),
\(+4a\), \(−2b\), \(−2c\), \(+5c\). Now, on grouping these
quantities together and striking a balance, it will be
seen that there are 8 of those things which are represented
by \(a\) on hand; likewise 4 more, represented by
\(4a\), on hand; 2 are owed, namely, \(−2a\). Therefore,
on grouping \(+8a\), \(+4a\), and \(−2a\) together, \(+10a\)
will be the result. Now, collecting those terms representing
the objects which we have called \(b\), we have
\(+6b\) and \(−2b\), giving as a result \(+4b\). Grouping
\(−3c\), \(−2c\), and \(+5c\) together will give 0, because
\(+5c\) represents \(5c\)’s on hand, and \(−3c\) and \(−2c\)
represent that \(5c\)’s are owed; therefore, these quantities
neutralize and strike a balance. Therefore,
\(+ 8a − 2a + 6b − 3c + 4a − 2b − 2c + 5c\)
reduces to
\(+10a + 4b\).
This process of gathering together and simplifying a
collection of terms having different signs is what we
call in algebra addition and subtraction. Nothing is
more simple, and yet nothing should be more thoroughly
understood before proceeding further. It is obviously
impossible to add one table to one chair and thereby
get two chairs, or one book to one hat and get two
books; whereas it is perfectly possible to add one book
to another book and get two books, one chair to another
chair and thereby get two chairs.
Rule. — Like symbols can be added and subtracted, and
only like symbols.
\(a + a\) will give \(2a\); \(3a\) + \(5a\) will give \(8a\); \(a + b\)
will not give \(2a\) or \(2b\), but will simply give \(a + b\),
this being the simplest form in which the addition of
these two terms can be expressed.
5
Coefficients. — In any term such as \(+8a\) the plus
sign indicates that the object is on hand or greater than
zero, the 8 indicates the number of them on hand, it
is the numerical part of the term and is called the
coefficient, and the \(a\) indicates the nature of the object,
whether it is a chair or a book or a table that we
have represented by the symbol \(a\). In the term \(+6a\),
the plus (+) sign indicates that the object is owned, or
greater than zero, the 6 indicates the number of objects
on hand, and the \(a\) their nature. If a man has \$20
in his pocket and he owes \$50, it is evident that if he
paid up as far as he could, he would still owe \$30. If
we had represented \$1 by the letter \(a\), then the \$20 in
his pocket would be represented by \(+20a\), the \$50
that he owed by \(−50a\). On grouping these terms
together, which is the same process as the settling of
accounts, the result would be \(−30a\).
Algebraic Expressions. — An algebraic expression consists
of two or more terms; for instance, \(+ a + b\) is
an algebraic expression; \(+ a + 2b + c\) is an algebraic
expression; \(+ 3a + 5b + 6b + c\) is another algebraic
expression, but this last one can be written more
simply, for the \(5b\) and \(6b\) can be grouped together in
one term, making \(11b\), and the expression now becomes
\(+ 3a + 11b + c\), which is as simple as it can be
written. It is always advisable to group together into
the smallest number of terms any algebraic expression
wherever it is met in a problem, and thus simplify the
manipulation or handling of it.
6
7
CHAPTER II
When there is no sign before the first term of an
expression the plus (+) sign is intended.
To subtract one quantity from another, change the
sign and then group the quantities into one term, as just
explained. Thus: to subtract \(4a\) from \(+ 12a\) we
write \(− 4a + 12a\), which simplifies into \(+ 8a\). Again,
subtracting \(2a\) from \(+ 6a\) we would have \(− 2a + 6a\),
which equals \(+4a\).
PROBLEMS
Simplify the following expressions:
1. \(10a + 5b + 6c − 8a − 3d + b\).
2. \(a − b + c − 10a − 7c + 2b\).
3. \(10d + 3z\) \(+ 8b − 4d\) \(− 6z − 12b\) \(+ 5a − 3d\)
\(+ 8z − 10a\) \(+ 8b\) \( − 5a − 6z\) \(+ 10b\).
4. \(5x − 4y\) \(+ 3z − 2x\) \(+ 4y\) \(+ x + z\) \(+ a − 7x\) \(+ 6y\).
5. \(3b − 2a\) \(+ 5c + 7a\) \(− 10b − 8c\) \(+ 4a − b\) \(+ c\).
6. \(− 2x + a\) \(+ b + 10y\) \(− 6x − y\) \(− 7a + 3b\) \(+ 2y\).
7. \(4x − y\) \(+ z + x\) \(+ 15z − 3x\) \(+ 6y − 7y\) \(+ 12z\).
CHAPTER II
Fundamentals of Algebra
Multiplication and Division
We have seen how the use of algebra simplifies the
operations of addition and subtraction, but in multiplication
and division this simplification is far greater, and
the great weapon of thought which algebra is to become
to the student is now realized for the first time. If the
student of arithmetic is asked to multiply one foot by
one foot, his result is one square foot, the square foot
being very different from the foot. Now, ask him to
multiply one chair by one table. How can he express
the result? What word can he use to signify the result?
Is there any conception in his mind as to the appearance
of the object which would be obtained by multiplying
one chair by one table? In algebra all this is
simplified. If we represent a table by \(a\), and a chair by
\(b\), and we multiply \(a\) by \(b\), we obtain the expression \(ab\),
which represents in its entirety the multiplication of a
chair by a table. We need no word, no name by which
to call it; we simply use the form \(ab\), and that carries
to our mind the notion of the thing which we call \(a\)
multiplied by the thing which we call \(b\). And thus the
form is carried without any further thought being given
to it.
8
Exponents. — The multiplication of \(a\) by \(a\) may be
represented by \(aa\). But here we have a further short
cut, namely, \(a^2\). This 2, called an exponent, indicates that
two \(a\)’s have been multiplied by each other; \(a × a × a\)
would give us \(a^3\), the 3 indicating that three \(a\)’s have
been multiplied by one another; and so on. The exponent
simply signifies the number of times the symbol has
been multiplied by itself.
Now, suppose \(a^2\) were multiplied by \(a^2\), the result would
be \(a^5\), since \(a^2\) signifies that 2 \(a\)’s are multiplied together,
and \(a^3\) indicates that 3 \(a\)’s are multiplied together; then
multiplying these two expressions by each other simply
indicates that 5 \(a\)’s are multiplied together. \(a^3 × a^7\)
would likewise give us \(a^{17}\), \(a^4 × a^4\) would give us \(a^8\),
\(a^4 × a^4 × a^2 × a^2\) would give us \(a^{12}\), and so on.
Rule. — The multiplication by each other of symbols
representing similar objects is accomplished by adding
their exponents.
9
Identity of Symbols. — Now, in the foregoing it must
be clearly seen that the combined symbol \(ab\) is different
from either \(a\) or \(b\); \(ab\) must be handled as differently
from \(a\) or \(b\) as \(c\) would be handled; in other words, it is
an absolutely new symbol. Likewise \(a^2\) is as different
from \(a\) as a square foot is from a linear foot, and \(a^3\) is
as different from \(a^2\) as one cubic foot is from one square
foot. \(a^2\) is a distinct symbol. \(a^3\) is a distinct symbol,
and can only be grouped together with other \(a^3\)’s. For
example, if an algebraic expression such as this were met:
\(a^2 + a + ab + a^3 + 3a^2 − 2a − ab\),
to simplify it we could group together the \(a^2\) and the
\(+ 3a^2\), giving \(+4a^2\); the \(+a\) and the \(−2a\) give \(−a\);
the \(+ab\) and the \(−ab\) neutralize each other; there is
only one term with the symbol \(a^3\). Therefore the
above expression simplified would be \(4a^2 − a + a^3\).
This is as simple as it can be expressed. Above all
things the most important is never to group unlike
symbols together by addition and subtraction. Remember
fundamentally that \(a\), \(b,\) \(ab\), \(a^2\), \(a^3\), \(a^4\), are all
separate and distinct symbols, each representing a
separate and distinct thing.
Suppose we have \(a × b × c\). It gives us the term
\(abc\). If we have \(a^2 × b\) we get \(a^2b\). If we have \(ab × ab\),
we get \(a^2b^2\). If we have \(2 ab × 2 ab\) we get \(4ab\);
\(6 a^2b^3 × 3c\), we get \(18 a^2b^3c\); and so on. Whenever two
terms are multiplied by each other, the coefficients are
multiplied together, and the similar parts of the symbols
are multiplied together.
10
Division. — Just as when in arithmetic we write
down \(\tfrac{2}{3}\) to mean 2 divided by 3, in algebra we write \(\tfrac{a}{b}\)
to mean \(a\) divided by \(b\). \(a\) is called a numerator and
\(b\) a denominator, and the expression \(\tfrac{a}{b}\) is called a fraction.
If \(a^3\) is multiplied by \(a^2\), we have seen that the
result is \(a^5\), obtained by adding the exponents 3 and 2.
If \(a^3\) is divided by \(a^2\), the result is \(a\), which is obtained
by subtracting 2 from 3. Therefore \(\tfrac{a^2b}{ab}\) would equal \(a\),
the \(a\) in the denominator dividing into \(a^2\) in the numerator
\(a\) times, and the \(b\) in the denominator canceling
the \(b\) in the numerator. Division is then simply the
inverse of multiplication, which is patent. On simplifying
such an expression as \(\tfrac{a^4b^2c^3}{a^2bc^5}\) we obtain \(\tfrac{a^2b}{c^2}\), and so on.
Negative Exponents. — But there is a more scientific
and logical way of explaining division as the inverse
of multiplication, and it is thus: Suppose we have the
fraction \(\tfrac{1}{a^2}\). This may be written \(a^{-2}\), or the term \(b^2\)
may be written \(\tfrac{1}{b^{-2}}\); that is, any term may be changed
from the numerator of a fraction to the denominator by
simply changing the sign of its exponent. For example,
\(\tfrac{a^5}{a^2}\) may be written \(a^5 × a^{-2}\). Multiplying these two
terms together, which is accomplished by adding their
exponents, would give us \(a^3\), 3 being the result of
the addition of 5 and −2. It is scarcely necessary,
therefore, to make a separate law for division if one is
made for multiplication, when it is seen that division
simply changes the sign of the exponent. This should
be carefully considered and thought over by the pupil,
for it is of great importance. Take such an expression
as \(\tfrac{a^2b^{-2}c^2}{abc^{-1}}\). Suppose all the symbols in the denominator
are placed in the numerator, then we have \(a^2b^{-2}c^2a^{-1}b^{-1}c\),
or, simplifying, \(ab^{-3}c^3\), which may be further written
\(\tfrac{ac^3}{b^3}\). The negative exponent is very serviceable, and it
is well to become thoroughly familiar with it. The following
examples should be worked by the student.
11
12
CHAPTER III
PROBLEMS
Simplify the following:
1. \(2a × 3b × 3ab\).
2. \(12a^2bc × 4c^2b\).
3. \(6x × 5y × 3xy\).
4. \(4a^2bc × 3abc × a^5b × 6b^2\).
5. \(\frac{a^2b^2c^3}{abc}\).
6. \(\frac{a^4b^3c^2d}{a^2d^2}\).
7. \(a^{-2} × b^3 × a^6b^2c\).
8. \(abc^2 × b^{-2}a^{-1}c^5 × a^3b^3\).
9. \(\frac{a^4b^{-6}c^3z}{a^2b^{-2}c}\).
10. \(10a^2b × 5a^{-1}bc^{-3} × \frac{8ac^{-1}}{b^2a^{-4}} × 10^{-1}a\).
11. \(\frac{5a^2b^2c^2d^2}{45a^3 × 6d^3}\).
CHAPTER III
Fundamentals of Algebra
Multiplication and Division Continued
HAVING illustrated and explained the principles of
multiplication and division of algebraic terms, we will
in this lecture inquire into the nature of these processes
as they apply to algebraic expressions. Before doing
this, however, let us investigate a little further into the
principles of fractions.
Fractions. — We have said that the fraction \(\tfrac{a}{b}\) indicated
that a was divided by b, just as in arithmetic
\(\tfrac{1}{3}\) indicates that 1 is divided by 3. Suppose we
multiply the fraction \(\tfrac{1}{3}\) by 3, we obtain \(\tfrac{3}{3}\), our procedure
being to multiply the numerator 1 by 3. Similarly,
if we had multiplied the fraction \(\tfrac{a}{b}\) by 3, our result
would have been \(\tfrac{3a}{b}\).
13
Rule. — The multiplication of a fraction by any quantity
is accomplished by multiplying its numerator by
that quantity; thus, \(\tfrac{2a^2}{b}\) multiplied by 3a would give
\(\tfrac{6a^2}{b}\). Conversely, when we divide a fraction by a
quantity, we multiply its denominator by that quantity.
Thus, the fraction \(\tfrac{a}{b}\) when divided by 2b gives \(\tfrac{a}{2b^2}\)
Finally, should we multiply the numerator and the
denominator by the same quantity, it is obvious that
we do not change the value of the fraction, for we have
multiplied and divided it by the same thing. From
this it must not be deduced that adding the same
quantity to both the numerator and the denominator of
a fraction will not change its value. The beginner is
likely to make this mistake, and he is here warned
against it. Suppose we add to both the numerator and
the denominator of the fraction \(\tfrac{1}{3}\) the quantity 2. We will
obtain \(\tfrac{3}{5}\), which is different in value from \(\tfrac{1}{3}\), proving
that the addition or subtraction of the same quantity
from both numerator and denominator of any fraction
changes its value. The multiplication or division of
both the numerator and the denominator by the same
quantity does not alter the value of a fraction one whit.
Multiplying two fractions by each other is accomplished
by multiplying their numerators together and
multiplying their denominators together. Thus, \(\tfrac{a}{b} × \tfrac{d}{c}\)
would give us \(\tfrac{ad}{bc}\).
14
Suppose it is desired to add the fraction \(\tfrac{1}{2}\) to the
fraction \(\tfrac{1}{3}\). Arithmetic teaches us that it is first necessary
to reduce both fractions to a common denominator,
which in this case is 6, viz.: \(\tfrac{3}{6} + \tfrac{2}{6} = \tfrac{5}{6}\), the numerators
being added if the denominators are of a common
value. Likewise, if it is desired to add \(\tfrac{a}{b}\) to \(\tfrac{c}{d}\), we must
reduce both of these fractions to a common denominator,
which in this case is \(bd\). (The common denominator of
several denominators is a quantity into which any one of
these denominators may be divided; thus b will divide into
\(bd\), d times, and d will divide into \(bd\), b times.) Our fractions
then become \(\tfrac{ad}{bd} + \tfrac{cb}{bd}\). The denominators now having a
common value, the fractions may be added by adding
the numerators, resulting in \(\tfrac{ad + cb}{bd}\). Likewise, adding
the fractions \(\tfrac{a}{3} + \tfrac{b}{2a} + \tfrac{c}{3a}\), we find that the common
denominator in this case is 6a. The first fraction
becomes \(\tfrac{2a^2}{6a}\) the second \(\tfrac{3b}{6a}\) and the third \(\tfrac{2c}{6a}\), the
result being the fraction \(\tfrac{2a^2 + 3b + 2c}{6a}\). This process
will be taken up and explained in more detail later, but
the student should make an attempt to apprehend the
principles here stated and solve the problems given at
the end of this lecture.
15
Law of Signs. — Like signs multiplied or divided give
+ and unlike signs give −. Thus:
\(+3a × +2a\) gives \(+ 6a^2\),
also \(−3a × −2a\) gives \(+ 6a^2\),
while \(+3a × −2a\) gives \(−6a^2\)
or \(−3a × + 2a\) gives \(−6a^2\);
furthermore \(+8a^2\) divided by \(+2a\) gives \(+4a\),
and \(−8a^2\) divided by \(−2a\) gives \(+4a\)
while \(−8a^2\) divided by \(+2a\) gives \(−4a\)
or \(+8a^2\) divided by \(−2a\) gives \(−4a\).
Multiplication of an Algebraic Expression by a
Quantity. — As previously said, an algebraic expression
consists of two or more terms. \(3a\), \(5b\), are terms,
but \(3a + 5b\) is an algebraic expression. If the stock
of a merchant consists of 10 tables and 5 chairs, and he
doubles his stock, it is evident that he must double the
number of tables and also the number of chairs, namely,
increase it to 20 tables and 10 chairs. Likewise, when
an algebraic expression which consists of \(3a + 2b\) is
doubled, or, what is the same thing, multiplied by 2,
each term must be doubled or multiplied by 2, resulting
in the expression \(6a + 4b\). Similarly, when an
algebraic expression consisting of several terms is
divided by any number, each term must be divided by
that number.
Rule. — An algebraic expression must be treated as a
unit. Whenever it is multiplied or divided by any quantity,
each term of the expression must be multiplied or
divided by that quantity. For example: Multiplying
the expression \(4x + 3y + 5xy\) by the quantity \(3x\) will
give the following result: \(12x^2 + 9xy + 15z^2y\), obtained
by multiplying each one of the separate terms by \(3x\)
successively.
16
Division of an Algebraic Expression by a Quantity. —
Dividing the expression \(6a^2 + 2a^2b + 4b^2\) by \(2ab\)
would result in the expression \(\tfrac{3a^2}{b} + a + \tfrac{2b}{a}\), obtained
by dividing each term successively by \(2b\). This rule
must be remembered, as its importance cannot be over-estimated.
The numerator or denominator of a fraction
consisting of one or two or more terms must be
handled as a unit, this being one of the most important
applications of this rule. For example, in the fraction
\(\tfrac{a + b}{a}\) or \(\tfrac{a}{a + b}\) it is impossible to cancel out the \(a\) in
the numerator and denominator, for the reason that if
the numerator is divided by \(a\), each term must be
divided by \(a\), and the operation upon the one term \(a\)
without the same operation upon the term \(b\) would
be erroneous. If the fraction \(\tfrac{a + b}{a}\) is multiplied by 3,
it becomes \(\tfrac{3a + 3b}{a}\). If the fraction \(\tfrac{a − b}{a + b}\) is multiplied
by \(\tfrac{2}{3}\) it becomes \(\tfrac{2a − 2b}{3a + 3b}\); and so on. Never
forget that the numerator (or denominator) of a fraction
consisting of two or more terms is an algebraic expression
and must be handled as a unit.
17

Workup 3-1

Workup 3-2

Workup 3-3
18

Workup 3-4
Multiplication of One Algebraic Expression by Another. —
It is frequently desired to multiply an algebraic
expression not only by a single term but by another
algebraic expression consisting of two or more terms, in
which case the first expression is multiplied throughout
by each term of the second expression. The terms which
result from this operation are then collected together
by addition and subtraction and the result expressed in
the simplest manner possible. Suppose it were desired
to multiply \(a + b\) by \(c + d\). We would first multiply
\(a + b\) by c, which would give us \(ac + bc\). Then we
would multiply \(a + b\) by d, which would give us
\(ad + bd\). Now, collecting the result of these two multiplications
together, we obtain \(ac + bc + ad + bd\), viz.:
a + b
c + d
_______
ac + bc
ad + bd
____________________
ac + bc + ad + bd
Workup 3-1
Again, let us multiply
2a + b − 3c
a + 2b − c
____________________
2a² + ab − 3ac
4ab + 2b² − 6bc
− 2ac − bc + 3c²
_____________________________________
Workup 3-2
and we have
\(2a² + 5ab − 5ac + 2b² − 7bc + 3c²\).
Workup 3-3
The Division of one Algebraic Expression by Another. —
This is somewhat more difficult to explain and understand
than the foregoing. In general it may be said
that, suppose we are required to divide the expression
\(6a^2 + 17ab + 12b^2\) by \(3a + 4b\), we would arrange
the expression in the following way:
6a² + 17ab + 12b² | 3a + 4b
|_________
6a² + 8ab 2a + 3b
____________________
9ab + 12b²
9ab + 12b²
Workup 3-4
\(3a\) will divide into \(6a^2\), \(2a\) times, and this is placed
in the quotient as shown. This \(2a\) is then multiplied
successively into each of the terms in the divisor, namely,
\(3a + 4b\), and the result, namely, \(6a^2 + 8ab\), is placed
beneath the dividend, as shown. A line is then drawn
and this quantity subtracted from the dividend, leaving
\(9ab\). The \(+12b^2\) in the dividend is now carried.
Again, we observe that \(3a\) in the divisor will divide into
\(9ab\), \(+3b\) times, and we place this term in the divisor.
Multiplying \(3b\) by each of the terms of the divisor, as
before, will give us \(9ab + 12b^2\); and, subtracting this
as shown, nothing remains, the final result of the division
then being the expression \(2a + 3b\).
This process should be studied and thoroughly understood
by the student.
19
21
CHAPTER IV
PROBLEMS
Solve the following problems:
1. Multiply the fraction \(\frac{3a^2b^3c}{4x^2}\)
by the quantity \(3x\).
2. Divide the fraction \(\frac{abc}{6d}\) by the quantity \(3a\).
3. Multiply the fraction \(\tfrac{a^2b^2c^2}{xy^3}\) by
the fraction \(\tfrac{a^2b^2}{6a}\) by
the fraction \(\tfrac{x^2y}{b}\).
4. Multiply the expression \(4x + 3y + 2z\) by the quantity \(5x\).
5. Divide the expression \(8a^2b + 4a^3b^3 − 2ab^2\) by
the quantity \(2ab\).
6. Multiply the expression \(a + b\) by the expression \(a − b\).
7. Multiply the expression \(2a + b − c\) by
the expression \(3a − 2b + 4c\).
8. Divide the expression \(a^2 − 2ab + b^2\) by \(a − b\).
9. Divide the expression \(a^3 + 3a^2b + 3ab^2 + b^3\) by \(a + b\).
10. Multiply the fraction \(\frac{a + b}{a − b}\) by
\(\frac{a − b}{a − b}\).
11. Multiply the fraction \(\frac{3a}{c + d}\) by
\(\frac{c − d}{2}\) by \(\frac{a + c}{a − c}\).
12. Multiply the fraction \(\frac{a^{-2}bc^3}{4}\) by
\(\frac{b}{3a^{-2}}\) by \(\frac{a}{b}\).
2013. Add together the fractions \(\frac{2a}{b}\)
\(+ \frac{b}{4} + \frac{c}{b}\).
14. Add together the fractions \(\frac{2}{3a^2}\)
\(− \frac{4}{2a} + \frac{c}{6}\).
15. Add together the fractions \(\frac{10a^2}{b}\)
\(+ \frac{b}{4b} − \frac{x}{2c} + \frac{d}{6}\).
16. Add together the fractions \(\frac{a + b}{2a}\)
\(+ \frac{b − c}{4b}\).
17. Add together the fractions \(\frac{a}{a + b}\)
\(− \frac{2}{5a}\).
CHAPTER IV
Fundamentals of Algebra
Factoring
Definition of a Factor. — A factor of a quantity is
one of the two or more parts which when multiplied
together give the quantity. A factor is an integral
part of a quantity, and the ability to divide and subdivide
a quantity, be it a single term or a whole expression,
into those factors whose multiplication has created
it, is very valuable.
Factoring. — Suppose we take the number 6. Its
factors are readily detected as 2 and 3. Likewise the
factors of 10 are 5 and 2. The factors of 18 are 9 and
2; or, better still, \(3 × 3 × 2\). The factors of 30 are
\(3 × 2 × 5\); and so on. The factors of the algebraic expression
\(ab\) are readily detected as a and b, because
their multiplication created the term \(ab\). The factors
of \(6abc\) are 3, 2, a, b and c. The factors of \(25ab\) are 5,
5, a and b, which are quite readily detected.
22
25
CHAPTER V
The factors of an expression consisting of two or more
terms, however, are not so readily seen and sometimes
require considerable ingenuity for their detection. Suppose
we have an algebraic expression in which all of
the terms have one or more common factors,—that is,
that one or more like factors appear in the make-up of
each term. It is often desirable in this case to remove
the common factors from the several terms, and in
order to do this without changing the value of any of
the terms, the common factor or factors are placed
outside of a parenthesis and the terms from which they
have been removed placed within the parenthesis in
their simplified form. Thus, in the algebraic expression
\(6a^2b + 3a^3\), \(3a^3\) is a common factor of both terms;
therefore we may write the expression, without changing
its value, in the following manner: \(3a^2(2b + a)\).
The term \(3a^2\) written outside of the parenthesis indicates
that it must be multiplied into each of the separate
terms within the parenthesis. Likewise, in the
expression \(12xy + 4^3 + 6x^2z + 8xz\), \(2x\) is a common
factor of each of the terms, and the expression may
be written \(2x (6 y + 2x^2 + 3xz + 4z)\). It is often
desirable to factor in this simple manner.
Still further suppose we have \(a^2 + ab + ac + bc\); we
can take a out of the first two terms and c out of the
last two, thus: \(a(a + b) + c(a + b)\). Now we have
two separate terms and taking \((a + b)\) out of each
we have \((a + b) × (a + c)\). Likewise, in the expression
\(6x^2 + 4xy − 3zx − 2zy\)
we have
\(2x(3x + 2y) − z(3x + 2y)\),
or,
\((3x + 2y) × (2x − z)\).23
Now, suppose we have the expression \(a^2 − 2ab + b^2\).
We readily detect that this quantity is the result of
multiplying \(a − b\) by \(a − b\); the first and last terms
are respectively the squares of a and b, while the
middle term is equal to twice the product of a and
b. Any expression where this is the case is a perfect
square; thus, \(9x^2 − 12xy + 4y^2\) is the square of
\(3x − 2y\), and may be written \((3x − 2y)^2\). Remembering
these facts, a perfect square is readily detected.
The product of the sum and difference of two terms
such as \((a + b) × (a − b)\) equals \(a^2 − b^2\); or, briefly,
the product of the sum and difference of two numbers
is equal to the difference of their squares.
By trial it is often easy to discover the factors of
algebraic expressions; for example, \(2a^2 + 7ab + 3b^2\) is
readily detected to be the product of \(2a + b\) and
\(a + 3b\).
PROBLEMS
Factor the following:
1. \(30 a^2b\).
2. \(48 a^4c\).
3. \(30 x^2y^4z^3\).
4. \(144 x^2a^2\).
5. \(\frac{12ab^2c^3}{4a^2b^2}\).
6. \(\frac{10xy^2}{2x^2y}\).
7. \(2a^2 + ab − 2ac − bc\).
248. \(3x^2 + xy + 3xc + cy\).
9. \(2x^2 + 5xy + 2xz + 5yz\).
10. \(a^2 − 2ab + b^2\).
11. \(4x^2 − 12xy + 9y^2\).
12. \(81a^2 + 90ab + 25b^2\).
13. \(16c^2 − 48ca + 36a^2\).
14. \(4x^3y + 5xzy^2 − 10xzy\).
15. \(30ab + 15abc − 5bc\).
16. \(81x^2y^2 − 25a^2\).
17. \(a^4 − 16b^4\).
18. \(144x^4y^2 − 64z^2\).
19. \(4a^2 − 8ac + 4c\).
20. \(16y^2 + 8xy + x^2\).
21. \(6y^2 − 5xy − 6x^2\).
22. \(4a^2 − 3ab − 10b^2\).
23. \(6y^2 − 13xy + 6x^2\).
24. \(2a^2 − 5ab − 3b^2\).
25. \(2a^2 + 9ab + 10b^2\).
CHAPTER V
Fundamentals of Algebra
Involution and Evolution
We have in a previous chapter discussed the process
by which we can raise an algebraic term and even a
whole algebraic expression to any power desired, by
multiplying it by itself. Let us now investigate the
method of finding the square root and the cube root
of an algebraic expression, as we are frequently called
upon to do.
The square root of any term such as \(a^2\), \(a^4\), \(a^6\),
and so on, will be, respectively, \(±a\), \(±a^2\), and
\(±a^3\), obtained by dividing the exponents by 2.
The plus-or-minus sign (\(±\)) shows that either \(+a\) or
\(−a\) when squared would give us \(±a^2\). On taking the
square root, therefore, the plus-or-minus sign (\(±\)) is
always placed before the root. This is not the case in
the cube root, however. Likewise, the cube root of
such terms as \(a^3\), \(a^6\), \(a^9\), and so on, would be respectively
a, \(a^2\) and \(a^3\), obtained by dividing the exponents
by 3. Similarly, the square root of \(4a^4b^6\) will be seen
to be \(±2a^2b^3\), obtained by taking the square root of
each factor of the term. And likewise the cube root
of \(−27a^9b^6\) will be \(−3a^3b^2\). These facts are so self-evident
that it is scarcely necessary to dwell upon them.
However, the detection of the square and the cube root
of an algebraic expression consisting of several terms is
by no means so simple.
26

Workup 5-1

Workup 5-2
27

Workup 5-3
28

Workup 5-4
29
CHAPTER VI
Square Root of an Algebraic Expression. — Suppose
we multiply the expression \(a + b\) by itself. We obtain
\(a^2 + 2ab + 6^2\). This is evidently the square of \(a + b\).
Suppose then we are given this expression and asked to
determine its square root. We proceed in this manner:
Take the square root of the first term and isolate it,
calling it the trial root. The square root of \(a^2\) is
a; therefore place a in the trial root. Now square
a and subtract this from the original expression, and
we have the remainder \(2ab + b^2\). For our trial divisor
we proceed as follows: Double the part of the root
already found, namely, a. This gives us \(2a\). \(2a\) will
go into \(2ab\), the first term of the remainder, b times.
Add b to the trial root, and the same becomes \(a + b\).
Now multiply the trial divisor by b, it gives us \(2ab + b^2\),
and subtracting this from our former remainder, we
have nothing left. The square root of our expression,
then, is seen to be \(a + b\), viz.:
a² + 2ab + b² | a + b
a² |________
_______________
2a + b | 2ab + b²
| 2ab + b²
|__________
Workup 5-1
Likewise we see that the square root of \(4a^2 + 12ab + 9b^2\)
is \(2a + 3b\), viz.:
4a² + 12ab + 9b² | 2a + 3b
4a² |________
____________________
4a + 3b | 2 ab + 9b²
| 2 ab + 9b²
|______________
Workup 5-2
The Cube Root of an Algebraic Expression. — If we
multiply \(a + b\) by itself three times, in other words,
cube the expression, we obtain \(a^3 + 3a^2b + 3ab^2 + b^2\).
It is evident, therefore, that if we had been given this
latter expression and asked to find its cube root, our
result should be \(a + b\). In finding the cube root, \(a + b\),
we proceed thus: We take the cube root of the first
term, namely, a, and place this in our trial root. Now
cube a, subtract the a thus obtained from the original
expression, and we have as a remainder \(3a^2b + 3ab^2 + b^2\).
Now our trial divisor will consist as follows: Square
the part of the root already found and multiply same
by 3. This gives us \(3a^2\). Divide \(3a^2\) into the first
term of the remainder, namely, \(3a^2b\), and it will go
b times. b then becomes the second term of the
root. Now add to the trial divisor three times the first
term of the root multiplied by the second term of the
root, which gives us \(3ab\). Then add the second term
of the root square, namely, \(b^2\). Our full divisor now
becomes \(3a^2 + 3ab + b^2\). Now multiply this full divisor
by b and subtract this from the former remainder, namely,
\(3a^2b + 3ab^2 + b^2\), and, having nothing left, we see that
the cube root of our original expression is \(a + b\), viz.:
a³ + 3a²b + 3ab² + b² | a + b
a³ |_______
____________________________
3a² + 3ab + b² | 3a²b + 3ab² + b²
| 3a²b + 3ab² + b²
|_____________________
Workup 5-3
Likewise the cube root of \(27x^3 + 27x^2 + 9x + 1\) is
seen to be \(3x + 1\), viz.:
27x³ + 27x² + 9x + 1 | 3x+ 1
27x³ |_______
_______________________
27x² + 9x + 1 | 27x² + 9x + 1
| 27x² + 9x + 1
|_________________
Workup 5-4
PROBLEMS
Find the square root of the following expressions:
1. \(16x^2 + 24xy + 9y^2\).
2. \(4a^2 + 4ab + b^2\).
3. \(36x^2 + 24xy + 4y^2\).
4. \(25a^2 − 20ab + 4b^2\).
5. \(a^2 + 2ab + 2ac + 2bc + b^2 + c^2\).
Find the cube root of the following expressions:
1. \(8x^3 + 36x^2y + 54xy^2 + 27y^3\).
2. \(x^3 + 6x^2y + 12xy^2 + 8y^3\).
3. \(27a^3 + 81a^2b + 81ab^2 + 27b^2\).
CHAPTER VI
Fundamentals of Algebra
Simple Equations
An equation is the expression of the equality of two
things; thus, \(a = b\) signifies that whatever we call a is
equal to whatever we call b; for example, one pile of
money containing \$100 in one shape or another is
equal to any other pile containing \$100. It is evident
that if a quantity is added to or subtracted from one
side of an equation or equality, it must be added to or
subtracted from the other side of the equation or equality,
in order to retain the equality of the two sides;
thus, if \(a = b\), then \(a + c = b + c\) and \(a − c = b − c\).
Similarly, if one side of an equation is multiplied
or divided by any quantity, the other side must be
multiplied or divided by the same quantity; thus,
if
\(a = b\),
then
\(ac = bc\)
and
\(\frac{a}{c} = \frac{b}{c}\).
Similarly, if one side of an equation is squared, the
other side of the equation must be squared in order to
retain the equality. In general, whatever is done to
one side of an equation must also be done to the other
side in order to retain the equality of both sides. The
logic of this is self-evident.
30
Transposition. — Suppose we have the equation
\(a + b = c\). Subtract b from both sides, and we have
\(a + b − b = c − b\). On the left-hand side of the equation
the \(+b\) and the \(−b\) will cancel out, leaving a, and
we have the result \(a = c − b\). Compare this with our
original equation, and we will see that they are exactly
alike except for the fact that in the one b is on the
left-hand side of the equation, in the other b is on
the right-hand side of the equation; in one case its sign
is plus, in the other case its sign is minus. This indicates
that in order to change a term from one side of
an equation to the other side it is simply necessary to
change its sign; thus,
\(a − c + b = d\)
may be transposed into the equation
\(a = c − b + d\),
or into the form
\(a − d = c − b\),
or into the form
\(−d = c − a − b\).
Any term may be transposed from one side of an equation
to the other simply by changing its sign.
31
Adding or Subtracting Two Equations. — When two
equations are to be added to one another their corresponding
sides are added to one another; thus, \(a + c = b\)
when added to \(a = d + e\) will give \(2a + c = b + d + e\).
Likewise \(3a + b = 2c\) when subtracted from
\(10a + 2b = 6c\) will yield \(7a + b = 4c\).
Multiplying or Dividing Two Equations by one Another. — When
two equations are multiplied or divided
by one another their corresponding sides must be multiplied
or divided by one another; thus, \(a = b\) multiplied by
\(c = d\) will give \(ac = bd\), also \(a = b\) divided by \(c = d\)
will give \(\tfrac{a}{c} = \tfrac{b}{d}\).
Solution of an Equation. — Suppose we have such an
equation as \(4x + 10 = 2x + 24\), and it is desired that
this equation be solved for the value of x; that is, that
the value of the unknown quantity x be found. In
order to do this, the first process must always be
to group the terms containing x on one side of the
equation by themselves and all the other terms in the
equation on the other side of the equation. In this
case, grouping the terms containing the unknown
quantity x on the left-hand side of the equation we
have
\(4x − 2x = 24 − 10\).
Now, collecting the like terms, this becomes
\(2x = 14\).
32
The next step is to divide the equation through by the
coefficient of x, namely, 2. Dividing the left-hand
side by 2, we have x. Dividing the right-hand side
by 2, we have 7. Our equation, therefore, has resolved
itself into
\(x = 7\).
We therefore have the value of x. Substituting this
value in the original equation, namely,
\(4x + 10 = 2x + 24\),
we see that the equation becomes
\(28 + 10 = 14 + 24\),
or
\(38 = 38\),
which proves the result.
The process above described is the general method of
solving for an unknown quantity in a simple equation.
Let us now take the equation
\(2cx + c = 40 − 5x\).
This equation contains two unknown quantities, namely,
c and x, either of which we may solve for. x is usually,
however, chosen to represent the unknown quantity,
whose value we wish to find, in an algebraic expression;
in fact, x, y and z are generally chosen to represent
unknown quantities. Let us solve for x in the above
equation. Again we group the two terms containing
x on one side of the equation by themselves and all
other terms on the other side, and we have
\(2cx + 5x = 40 − c\).
33
On the left-hand side of the equation we have two terms
containing x as a factor. Let us factor this expression
and we have
\(x(2c + 5) = 40 − c\).
Dividing through by the coefficient of x, which is the
parenthesis in this case, just as simple a coefficient to
handle as any other, and we have
\(x = \frac{40 − c}{2c + 5}\).
This final result is the complete solution of the equation
as to the value of x, for we have x isolated on
one side of the equation by itself, and its value on the
other side. In any equation containing any number of
unknown quantities represented by symbols, the complete
solution for the value of any one of the unknowns is
accomplished when we have isolated this unknown on one
side of the equation by itself. This is, therefore, the whole
object of our solution.
It is true that the value of a above shown still contains
an unknown quantity, c. Suppose the numerical
value of c were now given, we could immediately find
the corresponding numerical value of x; thus, suppose c
were equal to 2, we would have
\(x = \frac{40 − 2}{4 + 5}\).
or,
\(x = \frac{38}{9}\)
34
This is the numerical value of x, corresponding to the
numerical value 2 of c. It 4 had been assigned as
the numerical value of c we should have
\(x = \frac{40 − 4}{8 + 5} = \frac{36}{13}\).
Clearing of Fractions. — The above simple equations
contained no fractions. Suppose, however, that we are
asked to solve the equation
\(\frac{x}{4} + \frac{6}{2} = \frac{3x}{2} + \frac{5}{6}\).
Manifestly this equation cannot be treated at once in
the manner of the preceding example. The first step
in solving such an equation is the removal of all the
denominators of the fractions in the equation, this
step being called the Clearing of Fractions.
35

Workup 6-1
As previously seen, in order to add together the
fractions \(\tfrac{1}{2}\) and \(\tfrac{1}{3}\) we must reduce them to a common
denominator, 6. We then have \(\tfrac{3}{6} + \tfrac{2}{6} = \tfrac{5}{6}\). Likewise,
in equations, before we can group or operate upon any
one of the terms we must reduce them to a common
denominator. The common denominator of several
denominators is any number into which any one of the
various denominators will divide, and the least common
denominator is the smallest such number. The product
of all the denominators—that is, multiplying them all
together—will always give a common denominator, but
not always the least common denominator. The least
common denominator, being the smallest common denominator,
is always desirable in preference to a larger
number; but some ingenuity is needed frequently in
detecting it. The old rule of withdrawing all factors
common to at least two denominators and multiplying
them together, and then by what is left of the denominators,
is probably the easiest and simplest way to proceed.
Thus, suppose we have the denominators 6, 8,
9 and 4. 3 is common to both 6 and 9, leaving respectively
2 and 3. 2 is common to 2, 8 and 4, leaving
respectively 1, 4 and 2, and still further common to 4
and 2. Finally, we have removed the common factors
3, 2 and 2, and we have left in the denominators 1, 2,
3 and 1. Multiplying all of these together we have
72, which is the Least Common Denominator of these
numbers, viz.:
3 | 6, 8, 9, 4
|____________
2 | 2, 8, 3, 4
|____________
2 | 1, 4, 3, 2
|____________
1, 2, 3, 1
Workup 6-1
\(3 × 2 × 2 × 1 × 2 × 3 × 1 = 72\).
36
Having determined the Least Common Denominator,
or any common denominator for that matter, the next
step is to multiply each denominator by such a quantity
as will change it into the Least Common Denominator.
If the denominator of a fraction is multiplied by any
quantity, as we have previously seen, the numerator
must be multiplied by that same quantity, or the value
of the fraction is changed. Therefore, in multiplying
the denominator of each fraction by a quantity, we
must also multiply the numerator. Returning to the
equation which we had at the outset, namely,
\(\tfrac{x}{4} + \tfrac{6}{2} = \tfrac{3x}{2} + \tfrac{5}{6}\), we see that the common denominator here is 12.
Our equation then becomes
\(\tfrac{3x}{12} + \tfrac{36}{12} = \tfrac{18x}{12} + \tfrac{10}{12}\).
We have previously seen that the multiplication or
division of both sides of an equation by the same
quantity does not alter the value of the equation.
Therefore we can at once multiply both sides of this
equation by 12. Doing so, all the denominators disappear.
This is equivalent to merely canceling all the
denominators, and the equation is now changed to the
simple form \(3x + 36 = 18x + 10\). On transposition
this becomes
\(3x − 18x = 10 − 36\),
or
\(−15x = −26\),
or
\(−x = \frac{+26}{15}\),
or
\(+ x = \frac{+26}{15}\).
Again, let us now take the equation
\(\frac{2x}{5c} + \frac{10}{c^2} = \frac{x}{3}\).37
The least common denominator will at once be seen to
be \(15c^2\). Reducing all fractions to this common denominator
we have
\(\frac{6cx}{15c^2} + \frac{150}{15c^2} = \frac{5c^2x}{15c^2}\).
Canceling all denominators, we then have
\(6cx + 150 = 5c^2x\).
Transposing, we have
\(6cx − 5c^2x = −150\).
Taking x as a common factor out of both of the terms
in which it appears, we have
\(x(6c − 5c^2) = −150\).
Dividing through by the parenthesis, we have
\(\frac{−150}{6c − 5c^2}\)
This is the value of x. If some numerical value is
given to c, such as 2, for instance, we can then find
the corresponding numerical value of x by substituting
the numerical value of c in the above, and we have
\(x = \frac{−150}{12 − 20} = \frac{−150}{−8} = 18.75\).
In this same manner all equations in which fractions
appear are solved.
38
41
CHAPTER VII
PROBLEMS
Suppose we wish to make use of algebra in the solution
of a simple problem usually worked arithmetically,
taking, for example, such a problem as this: A man purchases
a hat and coat for \$15.00, and the coat costs
twice as much as the hat. How much did the hat cost?
We would proceed as follows: Let x equal the cost of
the hat. Since the coat cost twice as much as the hat,
then \(2x\) equals the cost of the coat, and \(x + 2x = 15\)
is the equation representing the fact that the cost of
the coat plus the cost of the hat equals \$15; therefore,
\(3x = \$15\), from which \(x = \$5\); namely, the cost of the
hat was \$5. \(2x\) then equals \$10, the cost of the coat.
Thus many problems may be attacked.
Solve the following equations:
1. \(6x − 10 + 4x + 3 = 2x + 20 − x + 15\).
2. \(x + 5 + 3x + 6 = − 10x + 25 + 8x\).
3. \(cx + 4 + x = cx + 8\). Find the numerical value of x if \(c = 3\).
4. \(\frac{x}{5} + 3 = \frac{8x}{2} + 4\).
5. \(\frac{4x}{3} + \frac{3x}{5} + \frac{7}{2}\) = \(\frac{11}{3} + x\).
6. \(\frac{x}{c} + \frac{10}{4c} = \frac{x}{3} + \frac{x}{12c}\). Find the numerical value of x if \(c = 3\).39
7. \(\tfrac{10c}{3} − \tfrac{cx}{c} + \tfrac{8}{5c}\) = \(\tfrac{3cx}{10} + \tfrac{15}{2c}\). Find the numerical value of x if \(c = 6\).
8. \(\frac{x}{a + b} − 2 + \frac{y}{3} = 1\).
9. \(\frac{2x}{a} + 3x + \frac{2}{a − b} = x − \frac{3}{a^2}\).
10. \(\frac{x}{a + b} + \frac{x}{a − b} = 10\).
11. Multiply \(ax + b = cx − b\) by \(2a − x = c + 10\).
12. Multiply \(\frac{a}{3} + b = \frac{c}{d}\) by \(x = y + 3\).
13. Divide \(a^2 − b^2 = c\) by \(a + b = c + 3\).
14. Divide \(2a = 10y\) by \(a = y + 2\).
15. Add \(2a + 10 = x + 3 − d\) to \(3a − 7 = 2d\).
16. Add \(4ax + 2y = −10x\) to \(2ax − 7y = 5\).
17. Add \(15z^2 + x = 5\) to \(3x = −10y + 7\).
18. Subtract \(2a − d = 8\) from \(8a + d = 12\).
19. Subtract \(3x + 7 = 15x^2 + y\) from \(6x + 5 = 18x^2\).
20. Subtract \(\frac{2x}{3a + b} + c = 7\) from \(\frac{10x}{5y} = 18\).
21. Multiply \(\frac{x}{3a + b} − \frac{x}{3} = c\) by \(\frac{x}{c − d} = \frac{2a + b}{c}\).
22. Solve the equation \(\frac{1}{x} = −\frac{1}{x + 1}\).
23. If a coat cost one-half as much as a gun and twice as much as a hat, and all cost together \$100, what is the cost of each?40
24. The value of a horse is \$15 more than twice the value of a carriage, and the cost of both is \$1000; what is the cost of each?
25. One-third of Anne’s age is 5 years less than one-half plus 2 years; what is her age?
26. A merchant has 10 more chairs than tables in stock. He sells four of each and adding up stock finds that he now has twice as many chairs as tables. How many of each did he have at first?
CHAPTER VII
Fundamentals of Algebra
Simultaneous Equations
As seen in the previous chapter, when we have a
simple equation in which only one unknown quantity
appears, such, for instance, as x, we can, by algebraic
processes, at once determine the numerical value
of this unknown quantity. Should another unknown
quantity, such as c, appear in this equation, in order
to determine the value of x some definite value must
be assigned to c. However, this is not always possible.
An equation containing two unknown quantities
represents some manner of relation between these
quantities. If two separate and distinct equations representing
two separate and distinct relations which exist
between the two unknown quantities can be found,
then the numerical values of the unknown quantities
become fixed, and either one can be determined without
knowing the corresponding value of the other. The
two separate equations are called simultaneous equations,
since they represent simultaneous relations between
the unknown quantity. The following is an
example:
42
\(x + y = 10\).
\(x − y = 4\).
The first equation represents one relation between \(x\)
and y. The second equation represents another relation
subsisting between \(x\) and \(y\). The solution for the numerical
value of \(x\), or that of \(y\), from these two equations,
consists in eliminating one of the unknowns, \(x\) or \(y\) as
the case may be, by adding or subtracting, dividing or
multiplying the equations by each other, as will be
seen in the following. Let us now find the value of
\(x\) in the first equation, and we see that this is
\(x = 10 − y\).
Likewise in the second equation we have
\(x = 4 + y\).
These two values of \(x\) may now be equated (things
equal to the same thing must be equal to each other),
and we have
\(10 − y = 4 + y\),
or,
\(−2y = 4 − 10\),
\(−2y = −6\),
\(+2y = +6\),
\(y = 3\).43
Now, this is the value of \(y\). In order to find the
value of \(x\), we substitute this numerical value of
\(y\) in one of the equations containing both \(x\) and \(y\),
such as the first equation, \(x + y = 10\). Substituting,
we have
\(x + 3 = 10\).
Transposing,
\(x = 10 − 3\),
\(x = 7\).
Here, then, we have found the values of both \(x\) and
\(y\), the algebraic process having been made possible
by the fact that we had two equations connecting the
unknown quantities.
The simultaneous equations above given might have
been solved likewise by simply adding both equations
together, thus:
Adding
\(x + y = 10\)
and
\(x − y = 4\),
we have
\(x + y + x − y = 14\).
Here \(+y\) and \(−y\) will cancel out, leaving
\(2x = 14\),
\(x = 7\).
Both of these processes are called elimination, the
principal object in solving simultaneous equations being
the elimination of unknown quantities until some equation
is obtained in which only one unknown quantity
appears.
44
We have seen that by simply adding two equations
we have eliminated one of the unknowns. But suppose
the equations are of this type:
(1) \(3x + 2y = 12\),
(2) \(x + y = 5\).
Now we can proceed to solve these equations in one of
two ways: first, to find the value of \(x\) in each equation
and then equate these values of \(x\), thus obtaining an
equation where only \(y\) appears as an unknown quantity.
But suppose we are trying to eliminate \(x\) from
these equations by addition; it will be seen that adding
will not eliminate \(x\), nor even will subtraction eliminate
it. If, however, we multiply equation (2) by 3, it becomes
\(3x + 3y = 15\).
Now, when this is subtracted from equation (1), thus:
\(3x + 2y = 12\)
\(3x + 3y = 15\)
________________
\(−y = −3\)
the terms in \(x\), \(+3x\) and \(+3x\) respectively, will eliminate,
\(3y\) minus \(2y\) leaves \(−y\), and 12 − 15 leaves −3,
or
\(−y = −3\),
therefore
\(+y = +3\).45
Just as in order to find the value of two unknowns
two distinct and separate equations are necessary to
express relations between these unknowns, likewise to
find the value of the unknowns in equations containing
three unknown quantities, three distinct and separate
equations are necessary. Thus, we may have the
equations
(1) \(x + y + z = 6\),
(2) \(x − y + 2z = 1\),
(3) \(x + 3 − 8 = 4\).
We now combine any two of these equations, for instance
the first and the second, with the idea of eliminating
one of the unknown quantities, as \(x\). Subtracting
equation (2) from (1), we will have
(4) \(2y − z = 5\).
Now taking any other two of the equations, such as the
second and the third, and subtracting one from the other,
with a view to eliminating \(x\), and we have
(5) \(−2y + 3z = −3\).
We now have two equations containing two unknowns,
which we solve as before explained. For instance, adding
them, we have
\(2z = 2\),
\( z = 1\).
Substituting this value of z in equation (4), we have
\(2y − 1 = 5\)46
\(2y = 6\),
\(y = 3\).
Substituting both of these values of z and y in equation
(1), we have
\(x + 3 + 1 = 6\),
\(x = 2\).
Thus we see that with three unknowns three distinct
and separate equations connecting them are necessary in
order that their values may be found. Likewise with
four unknowns four distinct and separate equations
showing relations between them are necessary. In each
case where we have a larger number than two equations,
we combine the equations together two at a time, each
time eliminating one of the unknown quantities, and,
using the resultant equations, continue in the same
course until we have finally resolved into one final
equation containing only one unknown. To find the
value of the other unknowns we then work backward,
substituting the value of the one unknown found in an
equation containing two unknowns, and both of these in
an equation containing three unknowns, and so on.
The solution of simultaneous equations is very important
and the student should practice on this subject
until he is thoroughly familiar with every one of these
steps.
47
48
CHAPTER VIII
PROBLEMS
Solve the following problems:
1. \(2x + y = 8\)
\(2y − x = 6\).
2. \(x + y = 7\)
\(3x − y = 13\).
3. \(4x = y + 2\)
\(x + y = 3\).
4. Find the value of \(x\), y and z in the following equations:
\(x + y + z = 10\),
\(2x + y − z = 9\),
\(x + 2y + z = 12\).
5. Find the value of \(x\), \(y\) and \(z\) in the following equations:
\(2x + 3y + 2z = 20\),
\(x + 3y + z = 13\),
\(x + y + 2z = 13\).
6. \(\frac{x}{3} + y = 10\),
\(y + \frac{x}{5} = y − 3\).
7. \(\frac{x}{4} + \frac{y}{3a} = 100x + a\) if \(a = 8\),
\(\frac{2x}{5} = y + 10\).
8. \(3x + y = 15\),
\(x = 6 + 7y\).
9. \(\tfrac{9x}{a + b} = \tfrac{y}{a − b} − 7\),
\(x + y = 5\)
if \(a = 6\), \(b = 5\).
10. \(3x − y + 6x = 8\),
\(y − 10 + 4y = x\).
CHAPTER VIII
Fundamentals of Algebra
Quadratic Equations
THUS far we have handled equations where the
unknown whose value we were solving for entered the
equation in the first power. Suppose, however, that
the unknown entered the equation in the second power;
for instance, the unknown \(x\) enters the equation thus,
\(x^2 = 12 − 2x^2\).
In solving this equation in the usual manner we obtain
\(3x^2 = 12\),
\(x^2 = 4\).
Taking the square root of both sides,
\(x = ± 2\).
We first obtained the value of \(x^2\) and then took the
square root of this to find the value of \(x\). The solution
of such an equation is seen to be just as simple in
every respect as a simple equation where the unknown
did not appear as a square. But suppose that we have
such an equation as this:
\(4x^2 + 8x = 12\).
49
We see that none of the processes thus far discussed
will do. We must therefore find some way of grouping
\(x^2\) and \(x\) together which will give us a single term in \(x\)
when we take the square root of both sides; this device
is called “Completing the square in \(x\).”
It consists as follows: Group together all terms in \(x^2\)
into a single term, likewise all terms containing \(x\) into
another single term. Place these on the left-hand side
of the equation and everything else on the right-hand
side of the equation. Now divide through by the
coefficient of \(x^2\). In the above equation this is 4. Having
done this, add to the right-hand side of the equation
the square of one-half of the coefficient of \(x\). If
this is added to one side of the equation it must likewise
be added to the other side of the equation. Thus:
\(4x^2 + 8x = 12\).
Dividing through by the coefficient of \(x^2\), namely 4, we
have
\(x^2 + 2x = 3\).
Adding to both sides the square of one-half of the
coefficient of \(x\), which is 2 in the term \(2x\),
\(x^2 + 2x + 1 = 3 + 1\).
The left-hand side of this equation has now been made
into the perfect square of \(x + 1\), and therefore may be
expressed thus:
\((x + 1)^2 = 4\).
Now taking the square root of both sides we have
\(x + 1 = ± 2\).
50
Therefore, using the plus sign of 2, we have
\(x = 1\).
Using the minus sign of 2 we have
\(x = −3\).
The student will note that there must, in the nature of
the case, be two distinct and separate roots to a quadratic
equation, due to the plus and minus signs above
mentioned.
To recapitulate the preceding steps, we have:
(1) Group all the terms in \(x^2\) and \(x\) on one side of the
equation alone, placing those in \(x^2\) first.
(2) Divide through by the coefficient of \(x^2\).
(3) Add to both sides of the equation the square of
one-half of the coefficient of the \(x\) term.
(4) Take the square root of both sides (the left-hand
side being a perfect square). Then solve as for a simple
equation in \(x\).
Example: Solve for \(x\) in the following equation:
\(4x^2 = 56 − 20x\),51
\(4x^2 + 20x = 56\),
\(x^2 + 5x = 14\),
\(x^2 + 5x + \tfrac{25}{4} = 14 + \tfrac{25}{4}\),
\(x^2 + 5x + \tfrac{25}{4} = \tfrac{81}{4}\),
\( \bigl (x + \tfrac{5}{2} \bigr )^2 = \tfrac{81}{4}\).
Taking the square root of both sides we have
\(x + \tfrac{5}{2} = ±\tfrac{9}{2}\),
\(x = ±\tfrac{9}{2} − \tfrac{5}{2}\),
\(x = 2\) or \(−7\),
Example: Solve for \(x\) in the following equation:
\(2x^2 − 4x + 5 = x^2 + 2x − 10 − 3x^2 + 33\),52
\(2x^2 − x^2 + 3x^2 − 4x − 2x = 33 − 10 − 5\),
\(4x^2 − 6x = 18\),
\(x^2 −\tfrac{6x}{4}6 = \tfrac{18}{4}\),
\(x^2 −\tfrac{3x}{2} = \tfrac{18}{4}\),
\(x^2 −\tfrac{3x}{2} + \tfrac{9}{16} = \tfrac{18}{4} + \tfrac{9}{16}\),
\( \bigl( x − \tfrac{3}{4} \bigr) ^2 = \tfrac{72}{16} + \tfrac{9}{16}\),
\( \bigl( x − \tfrac{3}{4} \bigr) ^2 = \tfrac{81}{16}\),
\(x − \tfrac{3}{4} = ± \tfrac{9}{4}\),
\(x = ± \tfrac{9}{4} + \tfrac{3}{4}\),
\(x = +3\) or \(−1\tfrac{1}{2}.\)
Solving an Equation which Contains a Root. — Frequently
we meet with an equation which contains a
square or a cube root. In such cases it is necessary to
get rid of the square or cube root sign as quickly as
possible. To do this the root is usually placed on one
side of the equation by itself, and then both sides are
squared or cubed, as the case may be, thus:
Example: Solve the equation
\(\sqrt{2x + 6} + 5a = 10\).
Solving for the root, we have
\(\sqrt{2x + 6} = 10 − 5a\).
Now squaring both sides we have
\(2x + 6 = 100 − 100a + 25a^2\),
or,
\(2x = 25a^2 − 100a + 100 − 6\),
\(x = \frac{(25a^2 − 100a + 94)}{2}\).
In any event, our prime object is first to get the square-root
sign on one side of the equation by itself if possible,
so that it may be removed by squaring.
53
55
CHAPTER IX
Or the equation may be of the type
\(2a + 1 = \frac{4}{\sqrt{a − x}}\).
Squaring both sides we have
\(4a^2 + 4a + 1 = \frac{16}{a − x}\)
Clearing fractions we have
\(−4a^2x − 4ax − x + a^2 + a = 16\)
\(−x(4a^2 + 4a + 1) = −4a^3 − 4a^2 − a + 16\)
\(x = \frac{4a^3 + 4a^2 + a − 16}{4a^2 + 4a + 1}\)
PROBLEMS
Solve the following equations for the value of \(x\):
1. \(5x^2 − 15x = −10\).
2. \(3x^2 + 4x + 20 = 44\).
3. \(2x^2 + 11 = x^2 + 4x + 7\).
4. \(x^2 + 4x = 2x + 2x^2 − 8\).
5. \(7x + 15 − 2^2 = 3x + 18\).
6. \(x^4 + 2x^2 = 24\).
7. \(x^2 + \frac{5x}{a} + 6x^2 = 10\).
8. \(\frac{x^2}{a} + \frac{x}{b} − 3 = 0\).
9. \(14 + 6x = \frac{4x^2}{2} + \frac{2x}{a} − 7\).
10. \(\frac{x^2}{a + b} − 3x = 2\).
11. \(3x^2 + 5x − 15 = 0\).
12. \((x + 2)^2 + 2(x + 2) = −1\).
13. \((x − 3)^2 − 10x + 7 = 0\).
14. \((x − a)^2 − (x + a)^2 = 3\).
15. \(\frac{x + a}{x − a} + \frac{x + b}{x − b} = 2\).54
16. \(\frac{3x + 7}{2} − \frac{x + 2}{6} = \frac{12}{x + 1}\).
17. \(\frac{x^2 − 2}{4x} = \frac{x + 3 2x}{8}\).
18. \(\frac{x^2 − x − 1}{4} = x^2 + 6\).
19. \(8 = \frac{64}{\sqrt{x + 1}}\).
20. \(\sqrt{x + a} + 10a = 15\).
21. \(\frac{x}{a} = \sqrt{x + 1}\).
22. \(3x + 5 = 2 + \sqrt{3x + 4}\).
CHAPTER IX
Fundamentals of Algebra
Variation
THIS is a subject of the utmost importance in the
mathematical education of the student of science. It
is one to which, unfortunately, too little attention is
paid in the average mathematical textbook. Indeed,
it is not infrequent to find a student with an excellent
mathematical training who has but vaguely grasped
the notions of variation, and still it is upon variation
that we depend for nearly every physical law.
Fundamentally, variation means nothing more than
finding the constants which connect two mutually
varying quantities. Let us, for instance, take wheat
and money. We know in a general way that the more
money we have the more wheat we can purchase.
This is a variation between wheat and money. But we
can go no further in determining exactly how many
bushels of wheat a certain amount of money will buy
before we establish some definite constant relation
between wheat and money, namely, the price per
bushel of wheat. This price is called the Constant of
the variation. Likewise, whenever two quantities are
varying together, the movement of one depending
absolutely upon the movement of the other, it is impossible
to find out exactly what value of one corresponds
with a given value of the other at any time,
unless we know exactly what constant relation subsists
between the two.
56
Where one quantity, \(a\), varies as another quantity,
namely, increases or decreases in value as another quantity,
b, we represent the fact in this manner:
\(a \propto b\).
Now, wherever we have such a relation we can immediately
write
\(a\) = some constant \(× b\),
\(a = k × b\).
If we observe closely two corresponding values of \(a\) and
\(b\), we can substitute them in this equation and find out
the value of this constant. This is the process which
the experimenter in a laboratory has resorted to in deducing
all the laws of science.
57
Experimentation in a laboratory will enable us to
determine, not one, but a long series of corresponding
values of two varying quantities. This series of values
will give us an idea of the nature of their variation.
We may then write down the variation as above shown,
and solve for the constant. This constant establishes
the relation between \(a\) and \(b\) at all times, and is therefore
all-important. Thus, suppose the experimenter in
a laboratory observes that by suspending a weight of
100 pounds on a wire of a certain length and size it
stretched one-tenth of an inch. On suspending 200
pounds he observes that it stretches two-tenths of an
inch. On suspending 300 pounds he observes that it
stretches three-tenths of an inch, and so on. He at
once sees that there is a constant relation between the
elongation and the weight producing it. He then
writes:
Elongation \(\propto\) weight.
Elongation = some constant \(×\) weight.
\(E = K × W\).
Now this is an equation. Suppose we substitute one of
the sets of values of elongation and weight, namely,
.3 of an inch and 300 lbs.
We have
.3 = \(K × 300\).
Therefore
\(K = .001\).
Now, this is an absolute constant for the stretch of that
wire, and if at any time we wish to know how much a
certain weight, say 500 lbs., will stretch that wire, we
simply have to write down the equation
\(E = K × W\).
Substituting
elong. = \(.001 × 500\),
and we have
elong. = \(.5\) of an inch.
Thus, in general, the student will remember that where
two quantities vary as each other we can change this
variation, which cannot be handled mathematically,
into an equation which can be handled with absolute
definiteness and precision by simply inserting a constant
into the variation.
58
Inverse Variation. — Sometimes we have one quantity
increasing at the same rate that another decreases;
thus, the pressure on a certain amount of air increases
as its volume is decreased, and we write
\(v \propto \frac{1}{p}\),
then
\(v \propto K × \frac{1}{p}\),
Wherever one quantity increases as another decreases,
we call this an inverse variation, and we express it in the
manner above shown. Frequently one quantity varies
as the square or the cube or the fourth power of the
other; for instance, the area of a square varies as the
square of its side, and we write
\(A \propto b^2\),
or
\(A = Kb^2\).
Again, one quantity may vary inversely as the square of
the other, as, for example, the intensity of light, which
varies inversely as the square of the distance from its
source, thus:
\(A \propto \frac{1}{d^2}\),
or
\(A = K\frac{1}{d^2}\),59Grouping of Variations. — Sometimes we have a quantity varying as one quantity and also varying as another quantity. In such cases we may group these two variations into a single variation. Thus, we say that
\(a \propto b\),
also
\(a \propto c\),
then
\(a \propto b × c\)
or,
\(a = K × b × c\).
This is obviously correct; for, suppose we say that the
weight which a beam will sustain in end-on compression
varies directly as its width, also directly as its depth,
we see at a glance that the weight will vary as the
cross-sectional area, which is the product of the width
by the depth.
Sometimes we have such variations as this:
\(a \propto b\),
also
\(a \propto \frac{1}{c}\),
then
\(a \propto \frac{b}{c}\).
This is practically the same as the previous case, with
the exception that instead of two direct variations we
have one direct and one inverse variation.
There is much interesting theory in variation, which,
however, is unimportant for our purposes and which
I will therefore omit. If the student thoroughly masters
the principles above mentioned he will find them
of inestimable value in comprehending the deduction
of scientific equations.
60
61
CHAPTER X

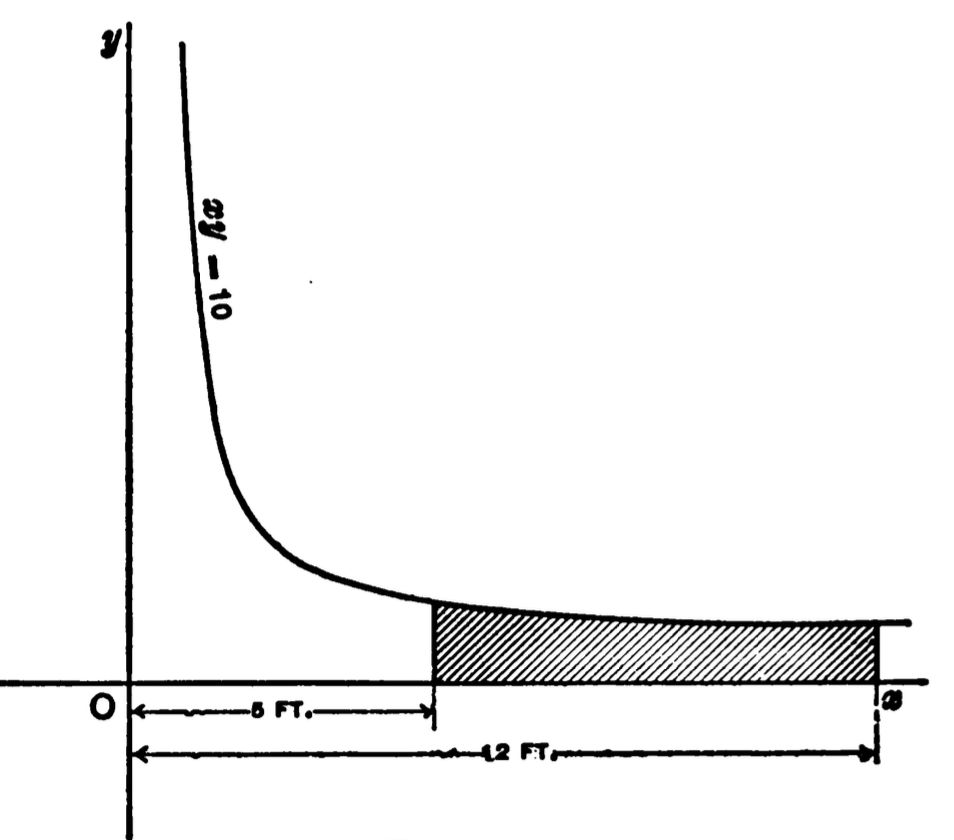
Fig. 1
62

Fig. 2

Fig. 3
63

Fig. 4

Fig. 5

Fig. 6

Fig. 7
64

Fig. 8
65

Fig. 9

Fig. 9a

Fig. 10

Fig. 11
PROBLEMS
1. If \(a \propto b\) and we have a set of values showing that when \(a = 500\), \(b = 10\), what is the constant of this variation?
2. If \(a \propto b^2\), and the constant of the variation is 2205, what is the value of \(b\) when \(a\) = 5?
3. \(a \propto b\); also \(a \propto \tfrac{1}{c}\), or, \(a \propto \tfrac{b}{c}\). If we find that when \(a = 100\), then \(b = 5\) and \(c = 3\), what is the constant of this variation?
4. \(a \propto b\). The constant of the variation equals 12. What is the value of \(a\) when \(b\) = 2 and \(c\) = 8?
5. \(a = K × \frac{b}{c}\). If K = 15 and \(a\) = 6 and \(b\) = 2, what is the value of \(c\)?
CHAPTER X
Some Elements of Geometry
In this chapter I will attempt to explain briefly some
elementary notions of geometry which will materially
aid the student to a thorough understanding of many
physical theories. At the start let us accept the following
axioms and definitions of terms which we will
employ.
Axioms and Definitions:
I. Geometry is the science of space.
II. There are only three fundamental directions or
dimensions in space, namely, length, breadth and depth.
III. A geometrical point has theoretically no dimensions.
IV. A geometrical line has theoretically only one
dimension,—length.
V. A geometrical surface or plane has theoretically
only two dimensions, namely, length and breadth.
VI. A geometrical body occupies space and has three
dimensions,—length, breadth and depth.
VI. An angle is the opening or divergence between
two straight lines which cut or intersect each other;
thus, in Fig. 1,
\(\measuredangle a\) is an angle between the lines \(AB\) and \(CD\), and may
be expressed thus, \(\measuredangle a\) or \(\measuredangle BOD\).
Fig. 1
VIII. When two lines lying in the same surface or
plane are so drawn that they never approach or retreat
from each other, no matter how long they are actually
extended, they are said to be parallel; thus, in Fig. 2,
the lines \(AB\) and \(CD\) are parallel.
Fig. 2
IX. A definite portion of a surface or plane bounded
by lines is called a polygon; thus, Fig. 3 shows a polygon.
Fig. 3
X. A polygon bounded by three sides is called a
triangle (Fig. 4).
Fig. 4
XI. A polygon bounded by four sides is called a
quadrangle (Fig. 5), and if the opposite sides are parallel,
a parallelogram (Fig. 6).
Fig. 5
Fig. 6
XII. When a line has revolved about a point until it
has swept through a complete circle, or 360°, it
comes back to its original
position. When it has revolved one quarter of a
circle, or 90°, away from its
original position, it is said
to be at right angles or
perpendicular to its original
position; thus, the angle \(a\) (Fig. 7) is a right angle
between the lines \(AB\) and \(CD\), which are perpendicular
to each other.
Fig. 7
XIII. An angle less than a right angle is called an
acute angle.
XIV. An angle greater than a right angle is called an
obtuse angle.
XV. The addition of two right angles makes a straight
line.
XVI. Two angles which when placed side by side or
added together make a right angle, or 90°, are said to
be complements of each other; thus, \(\measuredangle 30°\) and \(\measuredangle 60°\) are
complementary angles.
XVII. Two angles which when added together form
180°, or a straight line, are said to be supplements of
each other; thus, \(\measuredangle 130°\) and \(\measuredangle 50°\) are supplementary
angles.
XVIII. When one of the inside angles of a triangle is
a right angle, it is called a right-angle triangle (Fig. 8),
and the side AB opposite the right angle is called its
hypothenuse.
Fig. 8
XIX. A rectangle is a parallelogram whose angles
are all right angles (Fig. 9a), and a square is a rectangle
whose sides are all equal (Fig. 9).
Fig. 9
Fig. 9a
XX. A circle is a curved line, all points of which are
equally distant or equidistant from a fixed point called a
center (Fig. 10).
Fig. 10
Fig. 11
With these assumptions we may now proceed. Let us look at Fig. 11.
\(BM\) and \(CN\) are parallel lines cut by the common
transversal or intersecting line \(RS\). It is seen at a glance
that the \(\measuredangle ROM\) and \(\measuredangle BOA\), called vertical angles, are
equal; likewise \(\measuredangle ROM\) and
\(\measuredangle RAN\), called exterior interior angles, are equal;
likewise \(\measuredangle BOA\) and \(\measuredangle RAN\), called opposite interior
angles, are equal. These facts are actually
proved by placing one on the other, when they will
coincide exactly. The \(\measuredangle ROM\) and \(\measuredangle BOR\) are
supplementary, as their sum forms the straight line
\(BM\), or 180°. Likewise \(\measuredangle ROM\) and \(\measuredangle MOS\), or
\(\measuredangle NAS\), are supplementary.
66

Fig. 12

Fig. 18
70

Fig. 19
In general, we have this rule: When the corresponding
sides of any two angles are parallel to each other, the angles
are either equal or supplementary.
Fig. 12
Triangles. — Let us now investigate some of the properties
of the triangle \(ABC\) (Fig. 12). Through \(A\)
draw a line, \(MN\), parallel to \(BC\). At a glance we see
that the sum of the angles \(a\), \(d\), and \(e\) is equal to 180°,
or two right angles,—
\(\measuredangle a + \measuredangle d + \measuredangle e = 180°\)
But \(\measuredangle c\) is equal to \(\measuredangle d\), and \(\measuredangle b\) is equal to \(\measuredangle e\), as
previously seen; therefore we have
\(\measuredangle a + \measuredangle c + \measuredangle b = 180°\)
67

Fig. 13

Fig. 14
68

Fig. 15

Fig. 16
69
Fig. 17
This demonstration proves the fact that the sum of
all the inside or interior angles of any triangle is equal
to 180°, or, what is the same thing, two right angles.
Now, if the triangle is a right triangle and one of its
angles is itself a right angle, then the sum of the two
remaining angles must be equal to one right angle, or 90°.
This fact should be most carefully noted, as it is very
important.
When we have two triangles with all the angles of
the one equal to the corresponding angles of the other,
as in Fig. 13, they are called similar triangles.
Fig. 13
When we have two triangles with all three sides of
the one equal to the corresponding sides of the other,
they are equal to each other (Fig. 14), for they may be
perfectly superposed on each other. In fact, the two
triangles are seen to be equal if two sides and the included
angle of the one are equal to two sides and the
included angle of the other; or, if one side and two
angles of the one are equal to one side and the corresponding
angles respectively of the other; or, if one side
and the angle opposite to it of the one are equal to one
side and the corresponding angle of the other.
Fig. 14
Projections. — The projection of any given tract, such
as \(AB\) (Fig. I5), upon a line, such as \(MN\), is that space,
\(CD\), on the line \(MN\) bounded by two lines drawn
from \(A\) and \(B\) respectively perpendicular to \(MN\).
Fig. 15
Rectangles and Parallelograms. — A line drawn between
opposite corners of a parallelogram is called a
diagonal; thus, \(AC\) is a diagonal in Fig. 16. It is along
this diagonal that a body would move if pulled in the
direction of \(AB\) by one force, and in the direction \(AD\)
by another, the two forces having the same relative
magnitudes as the relative lengths of \(AB\) and \(AD\).
This fact is only mentioned here as illustrative of one
of the principles of mechanics.
Fig. 16
Fig. 17
The area of a rectangle is equal to the product of the
length by the breadth; thus, in Fig. 17,
Area of \(ABDC = AB × AC\).
This fact is so patent as not to need explanation.
Suppose we have a parallelogram (Fig. 18), however,
what is its area equal to?
The perpendicular distance \(BF\) between the sides \(BC\)
and \(AD\) of a parallelogram is called its altitude. Extend
the base \(AD\) and draw \(CE\) perpendicular to it.
Fig. 18
Now we have the rectangle \(BCEF\), whose area we know
to be equal to \(BC × BF\). But the triangles \(ABF\) and
\(DCE\) are equal (having 2 sides and 2 angles mutually
equal), and we observe that the rectangle is nothing else
than the parallelogram with the triangle \(ABF\) chipped
off and the triangle \(DCE\) added on, and since these are
equal, the rectangle is equal to the parallelogram, which
then has the same area as it; or,
Area of parallelogram \(ABCD = BC × BF\).
Fig. 19
If, now, we consider the area of the triangle \(ABC\)
(Fig. 19), we see that by drawing the lines \(AD\) and \(CD\)
parallel to \(BC\) and \(AB\) respectively, we have the parallelogram
\(BADC\), and we observe that the triangles \(ABC\)
and \(ADC\) are equal. Therefore triangle \(ABC\) equals
one-half of the parallelogram, and since the area of this
is equal to \(BC × AH\), then the
Area of the triangle \(ABC = \frac{1}{2} BC × AH\),
which means that the area of a triangle is equal to
one-half of the product of the base by the altitude.
71

Fig. 20

Fig. 21
72

Fig. 22
75
CHAPTER XI

Fig. 23
Circles. — Comparison between the lengths of the
diameter and circumference of a circle (Fig. 20) made
with the utmost care shows that
the circumference is 3.1416 times as
long as the diameter. This constant,
3.1416, is usually expressed
by the Greek letter pi (\(\pi \)). Therefore,
the circumference of a circle is
equal to \(\pi ×\) the diameter.
circum. = \(\pi d\)
circum. = \(2 \pi r\)
if \(r\), the radius, is used instead of the diameter.
Fig. 20
The area of a segment of a circle (Fig. 21), like the
area of a triangle, is equal to \(\tfrac{1}{2}\) of the product of the
base by the altitude, or \(\tfrac{1}{2}a × r\).
This comes from the fact that the
segment may be divided up into a
very large number of small segments
a whose bases, being very small, have
very little curvature, and may therefore
be considered as small triangles. Therefore, if we
consider the whole circle, where the length of the arc
is \(2\pi r\), the area is
\(\frac{1}{2} × 2\pi r × r = \pi r^2\),
Area circle\( = \pi r^2\).
Fig. 21
I will conclude this chapter by a discussion of one of
the most important properties of the right-angle triangle,
namely, that the square erected on its hypothenuse
is equal to the sum of the squares erected on
its other two sides; that is, that in the triangle \(ABC\)
(Fig. 22) \(\overline{AC}^2 = \overline{AB}^2 + \overline{BC}^2\).
Fig. 22
To prove
\(ANMC = BCRS + ABHK\),
or
length \(\overline{AC}^2\) = length \(\overline{BC}^2\) + length \(\overline{AB}^2\).73
This is a difficult problem and one of the most interesting
and historic ones that the whole realm of mathematics
can offer, therefore I will only suggest its solution
and leave a little reasoning for the student himself
to do.
triangle \(ARC\) = triangle BMC,
triangle \(ARC\) = \(\tfrac{1}{2}CR × BC\)
= \(\tfrac{1}{2}\) of the square \(BCRS\),
triangle \(BCM\) = \(\tfrac{1}{2} CM × CO\)
= \(\tfrac{1}{2} \)of rectangle \(COFM\).
Therefore
\(\frac{1}{2}\) of square \(BCRS\) = \(\frac{1}{2}\) of rectangle \(COFM\),
or
\(BCRS = COFM\).
Similarly for the other side
\(ABHK = AOFN\).
But
\(COFM + AOFN\) = whole square \(ACMN\).
Therefore
\(ACMN = BCRS + ABHK\).74
\((AC)^2 = (AB)^2 + (BC)^2\).
PROBLEMS
1. What is the area of a rectangle 8 ft. long by 12 ft. wide?
2. What is the area of a triangle whose base is 20 ft. and whose altitude is 18 ft.?
3. What is the area of a circle whose radius is 9 ft.?
4. What is the length of the hypothenuse of a right-angle triangle if the other two sides are respectively 6 ft. and 9 ft.? > 5. What is the circumference of a circle whose diameter is 20 ft.?
6. The hypothenuse of a right-angle triangle is 25 ft. and one side is 18 ft.; what is the other side?
7. If the area of a circle is 600 sq. ft., what is its diameter?
8. The circumference of the earth is 25,000 miles; what is its diameter in miles?
9. The area of a triangle is 30 sq. ft. and its base is 8 ft.; what is its altitude?
10. The area of a parallelogram is 100 sq. feet and its base is 25 ft.; what is its altitude?
CHAPTER XI
Elementary Principles of Trigonometry
TRIGONOMETRY is the science of angles; its province is
to teach us how to measure and employ angles with the
same ease that we handle lengths and areas.
Fig. 23
In a previous chapter we have defined an angle as the
opening or the divergence between two intersecting
lines, \(AB\) and \(CD\) (Fig. 23). The next question is, How
are we going to measure this angle? We have already
seen that we can do this in one way by employing
degrees, a complete circle being 360°. But there are
many instances which the student will meet later on
where the use of degrees would be meaningless. It
is then that certain constants connected with the angle,
called its functions, must be resorted to. Suppose we
have the angle \(a\) shown in Fig. 24. Now let us choose
a point anywhere either on the line \(AB\) or \(CD\); for
instance, the point \(P\). From \(P\) drop a line which will
be perpendicular to \(CD\). This gives us a right-angle
triangle whose sides we may call \(a\), \(b\) and \(c\) respectively.
We may now define the following functions of the \(\measuredangle a\):
76

Fig. 24
Fig. 24
sine \(\propto = \tfrac{a}{c}\),
cosine \(\propto = \tfrac{b}{c}\),
tangent \(\propto = \tfrac{a}{b}\),
which means that the sine of an angle is obtained by
dividing the side opposite to it by the hypothenuse; the
cosine, by dividing the side adjacent to it by the hypothenuse;
and the tangent, by dividing the side opposite
by the side adjacent.
These values, sine, cosine and tangent, are therefore
nothing but ratios,—pure numbers,—and under no circumstances
should be taken for anything else. This is
one of the greatest faults that I have to find with many
texts and handbooks in not insisting on this point.
77
Looking at Fig. 24, it is evident that no matter where
I choose \(P\), the values of the sine, cosine and tangent
will be the same; for if I choose \(P\) farther out on the
line I will increase \(c\), but at the same time \(a\) will increase
in the same proportion, the quotient of \(\tfrac{a}{c}\) being always
the same wherever \(P\) may be chosen.
Likewise \(\tfrac{b}{c}\) and \(\tfrac{a}{b}\) will always remain constant. The
sine, cosine, and tangent are therefore always fixed and
constant quantities for any given angle. I might have
remarked that if \(P\) had been chosen on the line \(CD\) and
the perpendicular drawn to \(AB\), as shown by the dotted
lines (Fig. 24), the hypothenuse and adjacent side simply
exchange places, but the value of the sine, cosine and
tangent would remain the same.
Since these functions, namely, sine, cosine and tangent,
of any angle remain the same at all times, they
become very convenient handles for employing the
angle. The sines, cosines and tangents of all angles of
every size may be actually measured and computed
with great care once and for all time, and then arranged
in tabulated form, so that by referring to this table one
can immediately find the sine, cosine or tangent of any
angle; or, on the other hand, if a certain value said to
be the sine, cosine or tangent of an unknown angle is
given, the angle that it corresponds to may be found
from the table. Such a table may be found at the end
of this book, giving the sines, cosines and tangents of
all angles taken 6 minutes apart. Some special compilations
of these tables give the values for all angles taken
only one minute apart, and some even closer, say 10 seconds
apart.
78
On reference to the table, the sine of 10° is .1736, the
cosine of 10° is .9848, the sine of 24° 36' is .4163, the cosine
of 24° 36' is .9092. In the table of sines and cosines
the decimal point is understood to be before every value,
for, if we refer back to our definition of sine and cosine,
we will see that these values can never be greater than
1; in fact, they will always be less than 1, since the
hypothenuse \(c\) is always the longest side of the right
angle and therefore \(a\) and \(b\) are always less than it.
Obviously, \(\tfrac{a}{c}\) and \(\tfrac{b}{c}\), the values respectively of sine and
cosine, being a smaller quantity divided by a larger,
can never be greater than 1. Not so with the tangent;
for angles between o° and 45°, \(a\) is less than \(b\),
therefore \(\tfrac{a}{b}\) is less than 1; but for angles between 45°
and 90°, \(a\) is greater than \(b\), and therefore \(\tfrac{a}{b}\) is greater
than 1. Thus, on reference to the table the tangent
of 10° 24' is seen to be .1835, the tangent of 45° is 1,
the tangent of 60° 30' is 1.7675.
79

Fig. 25

Fig. 26

Fig. 27
Now let us work backwards. Suppose we are given .3437
as the sine of a certain angle, to find the angle.
On reference to the table we find that this is the sine
of 20° 6', therefore this is the angle sought. Again,
suppose we have .8878 as the cosine of an angle, to find
the angle. On reference to the table we find that this
is the angle 27° 24'. Likewise suppose we are given
3.5339 as the tangent of an angle, to find the angle.
The tables show that this is the angle 74° 12'.
When an angle or value which is sought cannot be
found in the tables, we must prorate between the next
higher and lower values. This process is called interpolation,
and is merely a question of proportion. It will
be explained in detail in the chapter on Logarithms.
Relation of Sine and Cosine. — On reference to Fig.
25 we see that the sine \(\alpha = \tfrac{a}{c}\)
but if we take \(\beta \), the other
acute angle of the right-angle
triangle, we see that cosine
\(\beta = \tfrac{a}{c}\).
Fig. 25
Remembering, always the fundamental definition
of sine and cosine, namely,
sine = \(\frac{Opposite side}{Hypothenuse}\),
cosine = \(\tfrac{Adjacent side}{Hypothenuse}\), we see that the cosine \(\beta \) is equal to the same thing as the sine \(\alpha \), therefore
sine \(\alpha \) = cosine \(\beta \).
80
Now, if we refer back to our geometry, we will remember
that the sum of the three angles of a triangle
= 180°, or two right angles, and therefore in a right-angle
triangle \(\measuredangle \alpha + \measuredangle \beta = 90°\), or 1 right angle. In
other words \(\measuredangle \alpha \) and \(\measuredangle \beta \) are complementary angles.
We then have the following general law: “The sine of
an angle is equal to the cosine of its complement.” Thus,
if we have a table of sines or cosines from 0° to 90°, or
sines and cosines between 0° and 45°, we make use of
this principle. If we are asked to find the sine of 68°
we may look for the cosine of (90° − 68°), or 22°; or, if
we want the cosine of 68°, we may look for the sine of
(90° − 68°), or 22°.
Other Functions. — There are some other functions
of the angle which are seldom used, but which I will
mention here, namely,
Cotangent = \(\frac{b}{a}\),
Secant = \(\frac{c}{b}\),
Cosecant = \(\frac{c}{a}\).81
Other Relations of Sine and Cosine. — We have seen
that the sine \(\alpha = \tfrac{a}{c}\) and the cosine \(\alpha = \tfrac{b}{c}\). Also from
geometry
\(a^2 + b^2 = c^2\)
(1)
Dividing equation (1) by \(c^2\) we have
\(\frac{a^2}{c^2}\) + \(\frac{b^2}{c^2}\) = 1
But this is nothing but the square of the sine plus the
square of the cosine of \(\measuredangle \alpha \), therefore
\((\)sine \(\alpha )^2 + (\) cosine \(\alpha )^2 = 1\).
Other relations whose proof is too intricate to enter
into now are
sine \(2 \alpha = 2\ \sin \alpha \ \cos\ \alpha \),
cos \(2 \alpha = 1 − 2\ \sin^2 \alpha \),
or cos \(2 \alpha = cos^2 \alpha − \sin^2 \alpha \).
Fig. 26
Use of Trigonometry. — Trigonometry is invaluable
in triangulation of all kinds. When two sides or one
side and an acute angle of a right-angle triangle are
given, the other two sides can be easily found. Suppose
we wish to measure the distance \(BC\) across the
river in Fig. 26; we proceed as follows: First we lay off
and measure the distance \(AB\) along the shore; then by
means of a transit we sight perpendicularly across the
river and erect a flag at \(C\); then we sight from \(A\) to \(B\)
and from \(A\) to \(C\) and determine the angle \(\alpha \). Now, as
before seen, we know that
\(tangent\ \alpha = \frac{a}{b}\).
82
Suppose \(b\) had been 1000 ft. and \(\measuredangle \alpha \) was 40°, then
\(tangent\ 40° = \frac{a}{1000}\).
The tables show that the tangent of 40° is .8391;
then \(.8391 = \frac{a}{1000}\),
therefore \(a = 839.1 ft\).
Thus we have found the distance across the river to be
839.1 ft.
Fig. 27
Likewise in Fig. 27, suppose \(c\) = 300 and \(\measuredangle \alpha = 36°\),
to find \(a\) and \(b\). We have
\(sine\ \alpha = \frac{a}{c}\),
or
\(sine\ 36° = \frac{a}{300}\).
83
From the tables \(sine\ 36° = .5878\).
\(.5878 = \frac{a}{300}\)
\(a = .5878 × 300\),
or
\(a = 176.34 ft\).
Likewise
\(cosine\ \alpha = \frac{b}{c}\).
From table,
\(cosine\ 36' = .8090\),
therefore
\(.8090 = \frac{b}{300}\),
or
\(b = 242.7 ft\).
Now, if we had been told that \(a = 225\) and \(b = 100\), to
find \(\measuredangle \alpha \) and \(c\), we would have proceeded thus:
\(tangent\ \alpha = \frac{a}{b}\).
Therefore
\(tangent\ \alpha = \frac{225}{100}\),
\(tangent\ \alpha = 2.25\) ft.
The tables show that this corresponds to the angle \(66° 4'\).
Therefore
\(a = 66° 4'\).
Now to find \(c\) we have
\(sin\ a = \frac{a}{c}\),
\(sin\ 66° 4' = \frac{255}{c}\).
From tables, \(sine\ 66° 4' = .9140\),
therefore
\(.9140 = \frac{255}{c}\),
or
\(c = \frac{255}{.9140} = 248.5 ft\).
And thus we may proceed, the use of a little judgment
being all that is necessary to the solution of the most
difficult problems of triangulation.
84
85
CHAPTER XII
PROBLEMS
1. Find the sine, cosine and tangent of 32° 20'.
2. Find the sine, cosine and tangent of 81° 24'.
3. What angle is it whose sine is .4320?
4. What angle is it whose cosine is .1836?
5. What angle is it whose tangent is .753?
6. What angle is it whose cosine is .8755?
In a right-angle triangle—
7. If \(a\) = 300 ft. and \(\measuredangle \alpha \) = 30°, what are \(c\) and \(b\)?
8. If \(a\) = 500 ft. and \(b\) = 315 ft., what are \(\measuredangle \alpha \) and \(c\)?
9. If \(c\) = 1250 ft. and \(\measuredangle \alpha \) = 80°, what are \(b\) and \(a\)?
10. If \(b\) = 250 ft. and \(c\) = 530 ft., what are \(\measuredangle \alpha \) and \(a\)?
CHAPTER XII
Logarithms
I HAVE inserted this chapter on logarithms because
I consider a knowledge of them very essential to the
education of any engineer.
Definition. — A logarithm is the power to which we
must raise a given base to produce a given number.
Thus, suppose we choose 10 as our base, we will say
that 2 is the logarithm of 100, because we must raise 10 to
the second power—in other words, square it—in order
to produce 100. Likewise 3 is the logarithm of 1000,
for we have to raise 10 to the third power (thus, \(10^3\)) to
produce 1000. The logarithm of 10,000 would then be
4, and the logarithm of 100,000 would be 5, and so on.
The base of the universally used Common System of
logarithms is 10; of the Napierian or Natural System, \(e\)
or 2.7. The latter is seldom used.
86
We see that the logarithms of such numbers as 100,
1000, 10,000, etc., are easily detected; but suppose we
have a number such as 300, then the difficulty of finding
its logarithm is apparent. We have seen that \(10^2\)
is 100, and \(10^3\) equals 1000, therefore the number 300,
which lies between 100 and 1000, must have a logarithm
which lies between the logarithms of 100 and 1000,
namely 2 and 3 respectively. Reference to a table of
logarithms at the end of this book, which we will explain
later, shows that the logarithm of 300 is 2.4771,
which means that 10 raised to the 2.4771ths power will
give 300. The whole number in a logarithm, for example
the 2 in the above case, is called the characteristic;
the decimal part of the logarithm, namely, 4771, is
called the mantissa. It will be hard for the student to
understand at first what is meant by raising 10 to a
fractional part of a power, but he should not worry
about this at the present time; as he studies more
deeply into mathematics the notion will dawn on him
more clearly.
We now see that every number has a logarithm, no
matter how large or how small it may be; every number
can be produced by raising 10 to some power, and this
power is what we call the logarithm of the number.
Mathematicians have carefully worked out and tabulated
the logarithm of every number, and by reference
to these tables we can find the logarithm corresponding
to any number, or vice versa. A short table of logarithms
is shown at the end of this book.
Now take the number 351.1400; we find its logarithm
is 2.545,479. Like all numbers which lie between 100
and 1000 its characteristic is 2. The numbers which
lie between 1000 and 10,000 have 3 as a characteristic;
between 10 and 100, 1 as a characteristic. We therefore
have the rule that the characteristic is always one
less than the number of places to the left of the decimal
point. Thus, if we have the number 31875.12, we
immediately see that the characteristic of its logarithm
will be 4, because there are five places to the left of the
decimal point. Since it is so easy to detect the characteristic,
it is never put in logarithmic tables, the mantissa
or decimal part being the only part that the tables
need include.
87
If one looked in a table for a logarithm of 125.60, he
would only find .09,899. This is only the mantissa of
the logarithm, and he would himself have to insert the
characteristic, which, being one less than the number of
places to the left of the decimal point, would in this
case be 2; therefore the logarithm of 125.6 is 2.09,899.
Furthermore, the mantissæ of the logarithms of
3.4546, 34.546, 345.46, 3454.6, etc., are all exactly the
same. The characteristic of the logarithm is the only
thing which the decimal point changes, thus:
log 3.4546 = 0.538,398,
log 34.546 = 1.538,398,
log 345.46 = 2.538,398,
log 3454.6 = 3.538,398,
etc.
Therefore, in looking for the logarithm of a number,
first put down the characteristic on the basis of the
above rules, then look for the mantissa in a table,
neglecting the position of the decimal point altogether.
Thus, if we are looking for the logarithm of .9840, we
first write down the characteristic, which in this case
would be −1 (there are no places to the left of the
decimal point in this case, therefore one less than none
is −1). Now look in a table of logarithms for the
mantissa which corresponds to .9840, and we find this
to be .993,083; therefore
log .9840 = −1.993,083.
If the number had been 98.40 the logarithm would have
been +1.993,083.
88
When we have such a number as .084, the characteristic
of its logarithm would be −2, there being one
less than no places at all to the left of its decimal point;
for, even if the decimal point were moved to the right
one place, you would still have no places to the left of
the decimal point; therefore
log .00,386 = −3.586,587,
log 38.6 = 1.586,587,
log 386 = 2.586,587,
log 386,000 = 5.586,587.
Interpolation. — Suppose we are asked to find the
logarithm of 2468; immediately write down 3 as the
characteristic. Now, on reference to the logarithmic
table at the end of this book, we see that the logarithms
of 2460 and 2470 are given, but not 2468. Thus:
log 2460 = 3.3909,89
log 2468 = ?
log 2470 = 3.3927.
We find that the total difference between the two
given logarithms, namely 3909 and 3927, is 16, the
total difference between the numbers corresponding to
these logarithms is 10, the difference between 2460 and
2468 is 8; therefore the logarithm to be found lies \(\tfrac{8}{10}\)
of the distance across the bridge between the two given
logarithms 3909 and 3927. The whole distance across
is 16. \(\tfrac{8}{10}\) of 16 is 12.8. Adding this to 3909 we have
3921.8; therefore
log of 2468 = 3.39,218.
Reference to column 8 in the interpolation columns to the
right of the table would have given this value at once.
Many elaborate tables of logarithms may be purchased
at small cost which make interpolation almost unnecessary
for practical purposes.
Now let us work backwards and find the number if
we know its logarithm. Suppose we have given the
logarithm 3.6201. Referring to our table, we see that
the mantissa .6201 corresponds to the number 417; the
characteristic 3 tells us that there must be four places
to the left of the decimal point; therefore
3.6201 is the log of 4170.0.
90
Now, for interpolation we have the same principles
aforesaid. Let us find the number whose log is −3.7304.
In the table we find that
log 7300 corresponds to the number 5370,
log 7304 corresponds to the number ?
log 7308 corresponds to the number 5380.
Therefore it is evident that
7304 corresponds to 5375.
Now the characteristic of our logarithm is −3; from
this we know that there must be two zeros to the left
of the decimal point; therefore
−3.7304 is the log of the number .005375.
Likewise
−2.7304 is the log of the number .05375,
−7304 is the log of the number 5.375,
4.7304 is the log of the number 53,750.
Use of the Logarithm. — Having thoroughly understood
the nature and meaning of a logarithm, let us
investigate its use mathematically. It changes multiplication
and division into addition and subtraction; involution
and evolution into multiplication and division.
We have seen in algebra that
\(a^2 × a^5 = a^{5+2}\), or \(a^7\),
and that
\(\frac{a^8}{a^3} = a^{8-3}\), or \(a^5\).91
In other words, multiplication or division of like symbols
was accomplished by adding or subtracting their exponents,
as the case may be. Again, we have seen that
\((a^2)^2 = a^4\),
or
\(\sqrt[3]{a^6} = a^2\).
In the first case \(a^2\) squared gives \(a^4\), and in the second
case the cube root of \(a^6\) is \(a^2\); to raise a number to a
power you multiply its exponent by that power; to find
any root of it you divide its exponent by the exponent
of the root. Now, then, suppose we multiply 336 by
5380; we find that
log of \(336 = 10^{2.5263}\),
log of \(5380 = 10^{3.7308}\).
log of \(5380 = 10^{3.7308}\).
Then \(336 × 5380\) is the same thing as \(10^{2.5263} × 10^{3.7308}\),
But \(10^{2.5263} × 10^{3.7308} = 10^{2.526310 + 3.7308} = 10^{6.2571}\).
We have simply added the exponents, remembering that
these exponents are nothing but the logarithms of 336
and 5380 respectively.
Well, now, what number is \(10^{6.2571}\) equal to? Looking
in a table of logarithms we see that the mantissa .2571
corresponds to 1808; the characteristic 6 tells us
that there must be seven places to the left of the decimal;
therefore
\(10^{6.2571} =\) 1,808,000.92
If the student notes carefully the foregoing he will see
that in order to multiply 336 by 5380 we simply find
their logarithms, add them together, getting another
logarithm, and then find the number corresponding
to this logarithm. Any numbers may be multiplied
together in this simple manner; thus, if we multiply
\(217 × 4876 × 3.185 × .0438 × 890\), we have
log 217 = 2.3365
log 4876 = 3.6880
log 3.185 = .5031
log .0438 = −2.6415 [*]
log 890 = 2.9494
------
Adding we get
8.1185
[*] The −2 does not carry its negativity to the mantissa.
We must now find the number corresponding to the
logarithm 8.1185. Our tables show us that
8.1185 is the log of 131,380,000.
Therefore 131,380,000 is the result of the above multiplication.
To divide one number by another we subtract the
logarithm of the latter from the logarithm of the
former; thus, \(3865 ÷ 735\):
log 3865 = 3.5872
log 735 = 2.8663
______
.7209
The tables show that .7209 is the logarithm of 5.259;
therefore
\(3865 ÷ 735 = 5.259\).
93
As explained above, if we wish to square a number, we
simply multiply its logarithm by 2 and then find what
number the result is the logarithm of. If we had
wished to raise it to the third, fourth or higher power,
we would simply have multiplied by 3, 4 or higher power,
as the case may be. Thus, suppose we wish to cube
9879; we have
log 9897 = 3.9947
3
_____
11.9841
11.9841 is the log of 964,000,000,000;
therefore 9879 cubed = 964,000,000,000.
Likewise, if we wish to find the square root, the cube
root, or fourth root or any root of a number, we simply
divide its logarithm by 2, 3, 4 or whatever the root may
be; thus, suppose we wish to find the square root of
36,850, we have
log 36,850 = 4.5664.
4.5664 ÷ 2 = 2.2832.
4.5664 ÷ 2 = 2.2832.
2.2832 is the log. of 191.98; therefore the square root of
36,850 is 191.98.
The student should go over this chapter very carefully,
so as to become thoroughly familiar with the
principles involved.
94
95
CHAPTER XIII
PROBLEMS
1. Find the logarithm of 3872.
2. Find the logarithm of 73.56.
3. Find the logarithm of .00988.
4. Find the logarithm of 41,267.
5. Find the number whose logarithm is 2.8236.
6. Find the number whose logarithm is 4.87175.
7. Find the number whose logarithm is −1.4385.
8. Find the number whose logarithm is −4.3821.
9. Find the number whose logarithm is 3.36175.
10. Multiply 2261 by 4335.
11. Multiply 6218 by 3998.
12. Multiply 231.9 by 478.8 by 7613 by .921.
13. Multiply .00983 by .0291.
14. Multiply .222 by .00054.
15. Divide 27,683 by 856.
16. Divide 4337 by 38.88.
17. Divide .9286 by 28.75.
18. Divide .0428 by 1.136.
19. Divide 3995 by .003,337.
20. Find the square of 4291.
21. Raise 22.91 to the fourth power.
22. Raise .0236 to the third power.
23. Find the square root of 302,060.
24. Find the cube root of 77.85.
25. Find the square root of .087,64.
26. Find the fifth root of 226,170,000.
CHAPTER XIII
Elementary Principles of Coördinate Geometry
COÖRDINATE Geometry may be called graphic algebra,
or equation drawing, in that it depicts algebraic equations
not by means of symbols and terms but by means
of curves and lines. Nothing is more familiar to the
engineer, or in fact to any one, than to see the results of
machine tests or statistics and data of any kind shown
graphically by means of curves. The same analogy
exists between an algebraic equation and the curve
which graphically represents it as between the verbal
description of a landscape and its actual photograph;
the photograph tells at a glance more than could be
said in many thousands of words. Therefore the student
will realize how important it is that he master the
few fundamental principles of coördinate geometry which
we will discuss briefly in this chapter.
An Equation. — When discussing equations we remember
that where we have an equation which contains
two unknown quantities, if we assign some numerical
value to one of them we may immediately find the corresponding
numerical value of the other; for example, take
the equation
\(x = y + 4\).
96
In this equation we have two unknown quantities,
namely, \(x\) and \(y\); we cannot find the value of either
unless we know the value of the other. Let us say that
\(y = 1\); then we see that we would get a corresponding
value, \(x = 5\); for \(y = 2\), \(x = 6\); thus:
If \(y = 1\), then \(x = 5\),
\(y = 2\), \(x = 6\),
\(y = 3\), \(x = 7\),
\(y = 4\), \(x = 8\),
\(y = 5\), \(x = 9\), etc.
The equation then represents the relation in value
existing between \(x\) and \(y\), and for any specific value of
\(x\) we can find the corresponding specific value of \(y\).
Instead of writing down, as above, a list of such corresponding
values, we may show them graphically thus:
Draw two lines perpendicular to each other; make one
of them the \(x\) line and the other the \(y\) line. These two
lines are called axes. Now draw parallel to these axes
equi-spaced lines forming cross-sections, as shown in
Fig. 28, and letter the intersections of these lines with
the axes 1, 2, 3, 4, 5, 6, etc., as shown.
97

Fig. 28
98
Now let us plot the corresponding values, \(y = 1\),
\(x = 5\). This will be a point 1 space up on the \(y\) axis
and 5 spaces out on the \(x\) axis, and is denoted by letter
\(A\) in the figure. In plotting the corresponding values
\(y = 2\), \(x = 6\), we get the point \(B\); the next set of values
gives us the point \(C\), the next \(D\), and so on. Suppose
we draw a line through these points; this line, called
the curve of the equation, tells everything in a graphical
way that the equation does algebraically. If this line
has been drawn accurately we can from it find out at
a glance what value of \(y\) corresponds to any given value
of \(x\), and vice versa. For example, suppose we wish to
see what value of \(y\) corresponds to the value \(x = 6\tfrac{1}{2}\);
we run our eyes along the x axis until we come to \(6\tfrac{1}{2}\),
then up until we strike the curve, then back upon the
y axis, where we note that \(y = 2\tfrac{1}{2}\).
Fig. 28
Negative Values of x and y. — When we started at o
and counted 1, 2, 3, 4, etc., to the right along the x
axis, we might just as well have counted to the left,
−1, −2, −3, −4, etc. (Fig. 28), and likewise we
might have counted downwards along the y axis, −1,
−2, −3, −4, etc. The values, then, to the left of o
on the x axis and below o on the y axis are the negative
values of x and y. Still using the equation x = y + 4,
let us give the following values to y and note the corresponding
values of x in the equation x = y + 4:
If \(y = 0\), then \(x = 4\),
\(y = −1\), \(x = 3\),
\(y = −2\), \(x = 2\),
\(y = −3\), \(x = 1\),
\(y = −4\), \(x = 0\),
\(y = −5\), \(x = −1\),
\(y = −6\), \(x = −2\),
\(y = −7\), \(x = −3\).
The point \(y = 0, x = 4\) is seen to be on the \(x\) axis at
the point 4. The point \(y = −1, x = 3\) is at point \(E\),
that is, 1 below the \(x\) axis and 3 to the right of the \(y\)
axis. The points \(y = −2, x = 2\) and \(y = −3, x = 1\)
are seen to be respectively points \(F\) and \(G\). Point
\(y = −4, x = 0\) is zero along the \(x\) axis, and is therefore
at −4 on the \(y\) axis. Point \(y = −5, x = −1\)
is seen to be 5 below 0 on the \(y\) axis and 1 to
the left of 0 along the \(x\) axis (both \(x\) and \(y\) are now
negative), namely, at the point \(H\). Point
\(y = −6, x = −2\) is at \(J\), and so on.
99
The student will note that all points in the first
quadrant have positive values for both \(x\) and \(y\), all
points in the second quadrant have positive values for
\(y\) (being all above 0 so far as the \(y\) axis is concerned),
but negative values for \(x\) (being to the left of 0), all
points in the third quadrant have negative values
for both \(x\) and \(y\), while all points in the fourth quadrant
have positive values of \(x\) and negative values of \(y\).
Coördinates. — The corresponding \(x\) and \(y\) values of
a point are called its coördinates, the vertical or \(y\) value
is called its ordinate, while the horizontal or \(x\) value is
called the abscissa; thus at point \(A\), \(x = 5, y = 1\), here
5 is called the abscissa, while 1 is called the ordinate of
point \(A\). Likewise at point \(G\), where \(y = −3, x = 1\),
here −3 is the ordinate and 1 the abscissa of \(G\).
Straight Lines. — The student has no doubt observed
that all points plotted in the equation \(x = y + 4\) have
fallen on a straight line, and this will always be the case
where both of the unknowns (in this case \(x\) and \(y\)) enter
the equation only in the first power; but the line will
not be a straight one if either \(x\) or \(y\) or both of them
enter the equation as a square or as a higher power; thus,
\(x^2 = y + 4\) will not plot out a straight line because we
have \(x^2\) in the equation. Whenever both of the unknowns
in the equation which we happen to be plotting
(be they \(x\) and \(y\), \(a\) and \(b\), \(x\) and \(a\), etc.) enter the
equation in the first power, the equation is called a
linear equation, and it will always plot a straight line;
thus, \(3x + 5y = 20\) is a linear equation, and if plotted
will give a straight line.
100
Conic Sections. — If either or both of the unknown
quantities enter into the equation in the second power,
and no higher power, the equation will always represent
one of the following curves: a circle or an ellipse, a
parabola or an hyperbola. These curves are called the
conic sections. A typical equation of a circle is \(x^2 + x^2\)
= \(r^2\); a typical equation of a parabola is \(y^2 = 4qx\); a
typical equation of a hyperbola is \(x^2 − y^2 = r^2\), or,
also, \(xy = c^2\).
It is noted in every one of these equations that we
have the second power of \(x\) or \(y\), except in the equation
\(xy = c^2\), one of the equations of the hyperbola. In this
equation, however, although both \(x\) and \(y\) are in the
first power, they are multiplied by each other, which
practically makes a second power.
I have said that any equation containing \(x\) or \(y\) in
the second power, and in no higher power, represents
one of the curves of the conic sections whose type forms
we have just given. But sometimes the equations do
not correspond to these types exactly and require some
manipulation to bring them into the type form.
101

Fig. 29

Fig. 30
102
Let us take the equation of a circle, namely,
\(x^2 + y^2 = 5^2\), and plot it as shown in Fig. 29.
Fig. 29
We see that it is a circle with its center at the intersection
of the coördinate axes. Now take the equation
\((x − 2)^2 + (y − 3)^2 = 5^2\). Plotting this, Fig. 30,
we see that it is the same circle with its center at the
point whose coördinates are 2 and 3. This equation
and the first equation of the circle are identical in form,
but frequently it is difficult at a glance to discover this
identity, therefore much ingenuity is frequently required
in detecting same.
Fig. 30
In plotting the equation of a hyperbola, \(xy = 25\)
(Fig. 31), we recognize this as a curve which is met
with very frequently in engineering practice, and a
knowledge of its general laws is of great value.
Similarly, in plotting a parabola (Fig. 32), \(y^2 = 4x\),
we see another familiar curve.
In this brief chapter we can only call attention to the
conic sections, as their study is of academic more than
of pure engineering interest. However, as the student
progresses in his knowledge of mathematics, I would
suggest that he take up the subject in detail as one
which will offer much fascination.
103

Fig. 31

Fig. 32
104

Fig. 33
Fig. 31
Fig. 32
Other Curves. — All other equations containing unknown
quantities which enter in higher powers than the
second power, represent a large variety of curves called
cubic curves.
The student may find the curve corresponding to
engineering laws whose equations he will hereafter
study. The main point of the whole discussion of this
chapter is to teach him the methods of plotting, and if
successful in this one point, this is as far as we shall go
at the present time.
Intersection of Curves and Straight Lines. — When
studying simultaneous equations we saw that if we had
two equations showing the relation between two unknown
quantities, such for instance as the equations
\(x + y = 7\),
\(x − y = 3\).
\(x − y = 3\).
we could eliminate one of the unknown quantities in
these equations and obtain the values of \(x\) and \(y\) which
will satisfy both equations; thus, in the above equations,
eliminating \(y\), we have
\(2x = 10\),
\(x = 5\).
105
\(x = 5\).
Substituting this value of x in one of the equations, we
have
\(y = 2\).
Now each one of the above equations represents a
straight line, and each line can be plotted as shown in
Fig. 33.
Fig. 33
Their point of intersection is obviously a point on
both lines. The coördinates of this point, then, \(x = 5\)
and \(y = 2\), should satisfy both equations, and we have
already seen this. Therefore, in general, where we
have two equations each showing a relation in value
between the two unknown quantities, x and y, by combining
these equations, namely, eliminating one of the
unknown quantities and solving for the other, our
result will be the point or points of intersection of both
curves represented by the equations. Thus, if we add
the equations of two circles,
\(x^2 + y^2 = 4^2\),
\((x − 2)^2 + y^2 = 5^2\),
\((x − 2)^2 + y^2 = 5^2\),
and if the student plots these equations separately and
then combines them, eliminating one of the unknown
quantities and solving for the other, his results will be
the points of intersection of both curves.
106
Plotting of Data. — When plotting mathematically
with absolute accuracy the curve of an equation, whatever
scale we use along one axis we must employ along
the other axis. But, for practical results in plotting
curves which show the relative values of several varying
quantities during a test or which show the operation
of machines under certain conditions, we depart
from mathematical accuracy in the curve for the sake
of convenience and choose such scales of value along
each axis as we may deem appropriate. Thus, suppose
we were plotting the characteristic curve of a shunt
dynamo which had given the following sets of values
from no load to full load operation:
107

Fig. 34
| VOLTS | AMPERES |
| 122 | 0 |
| 120 | 5 |
| 118 | 10 |
| 116 | 15 |
| 114 | 19 |
| 111 | 22 |
| 107 | 25 |
Fig. 34
We plot this curve for convenience in a manner as
shown in Fig. 34. Along the volts axis we choose a
scale which is compressed to within one-half of the
space that we choose for the amperes along the ampere
axis. However, we might have chosen this entirely at
our own discretion and the curve would have had the
same significance to an engineer.
108
110
CHAPTER XIV
PROBLEMS
Plot the curves and lines corresponding to the following
equations:
1. \(x = 3y + 10\).
2. \(2x + 5y = 15\).
3. \(x − 2y = 4\).
4. \(10y + 3x = −8\).
5. \(x^2 + y^2 = 36\).
6. \(x^2 = 16y\).
7. \(x^2 − y^2 = 16\).
8. \(3x^2 + (y − 2)^2 = 25\).
Find the intersections of the following curves and
lines:
1. \(3x + y = 10\),
\(4x − y = 6\).
2. \(x^2 + y^2 = 81\),
\(x − y = 10\).
3. \(xy = 40\),109
\(3x + y = 5\).
Plot the following volt-ampere curve:
| VOLTS | AMPERES |
| 550 | 0 |
| 548 | 20 |
| 545 | 39 |
| 541 | 55 |
| 536 | 79 |
| 529 | 91 |
| 521 | 102 |
| 510 | 115 |
CHAPTER XIV
Elementary Principles of the Calculus
It is not my aim in this short chapter to do more
than point out and explain a few of the fundamental
ideas of the calculus which may be of value to a
practical working knowledge of engineering. To the
advanced student no study can offer more intellectual
and to some extent practical interest than the advanced
theories of calculus, but it must be admitted
that very little beyond the fundamental principles ever
enter into the work of the practical engineer.
In a general sense the study of calculus covers an investigation
into the innermost properties of variable quantities,
that is quantities which have variable values as
against those which have absolutely constant, perpetual
and absolutely fixed values. (In previous chapters we
have seen what was meant by a constant quantity and
what was meant by a variable quantity in an equation.)
By the innermost properties of a variable quantity we mean
finding out in the minutest detail just how this quantity
originated; what infinitesimal (that is, exceedingly small)
parts go to make it up; how it increases or diminishes
with reference to other quantities; what its rate of
increasing or diminishing may be; what its greatest
and least values are; what is the smallest particle into
which it may be divided; and what is the result of
adding all of the smallest particles together. All of
the processes of the calculus therefore are either analysis
or synthesis, that is, either tearing up a quantity
into its smallest parts or building up and adding
together these smallest parts to make the quantity.
We call the analysis, or tearing apart, differentiation;
we call the synthesis, or building up, integration.
111

Fig. 35
112
Fig. 36
DIFFERENTIATION
Suppose we take the straight line (Fig. 35) of length
\(x\). If we divide it into a large number of parts, greater
than a million or a billion or any number of which we
have any conception, we say that each part is infinitesimally
small,—that is, it is small beyond conceivable
length. We represent such inconceivably small lengths
by an expression \(\Delta x\) or \(\delta x\). Likewise, if we have a
surface and divide it into infinitely small parts, and if
we call \(a\) the area of the surface, the small infinitesimal
portion of that surface we represent by \(\Delta a\) or \(\delta a\).
These quantities, namely, \(\delta x\) and \(\delta a\), are called the
differential of \(x\) and \(a\) respectively.
Fig. 35
Fig. 36
We have seen that the differential of a line of the
length \(x\) is \(\delta x\). Now suppose we have a square each of
whose sides is \(x\), as shown in Fig. 36. The area of that
square is then \(x^2\). Suppose now we increase the length
of each side by an infinitesimally small amount, \(\delta x\),
making the length of each side \(x + \,\delta x\). If we complete
a square with this new length as its side, the new square
will obviously be larger than the old square by a very
small amount. The actual area of the new square will
be equal to the area of the old square + the additions
to it. The area of the old square was equal to \(x^2\).
The addition consists of two fine strips each \(x\) long by
\(\delta x\) wide and a small square having \(\delta x\) as the length of
its side. The area of the addition then is
\((x × \,\delta x) + (x × \,\delta x) + (\,\delta x × \,\delta x)\) = additional area.
(The student should note this very carefully.) Therefore
the addition equals
\(2x\,\delta x + (\,\delta x)^2\) = additional area.
113
Now the smaller \(\delta x\) becomes, the smaller in more rapid
proportion does \(\delta x^2\), which is the area of the small
square, become. Likewise the smaller \(\delta x\) is, the thinner
do the strips whose areas are \(x\,\delta x\) become; but the strips
do not diminish in value as fast as the small square
diminishes, and, in fact, the small square vanishes so
rapidly in comparison with the strips that even when
the strips are of appreciable size the area of the small
square is inappreciable, and we may say practically that
by increasing the length of the side \(x\) of the square
shown in Fig. 36 by the length \(\delta x\) we increase its area
by the quantity \(2x\,\delta x\).
Again, if we reduce the side \(x\) of the square by the
length \(\delta x\), we reduce the area of the square by the
amount \(2x\,\delta x\). This infinitesimal quantity, out of a
very large number of which the square consists or may
be considered as made up of, is equal to the differential of
the square, namely, the differential of \(x^2\). We thus see
that the differential of the quantity \(x^2\) is equal to \(2x\,\delta x\).
Likewise, if we had considered the case of a cube instead
of a square, we would have found that the differential of
the cube \(x^3\) would have been \(3x^2\,\delta x\). Likewise, by more
elaborate investigations we find that the differential of
\(x^4 = 4x^3\,\delta x\). Summarizing, then, the foregoing results
we have
differential of \(x = \,\delta x\),114
differential of \(x^2 = 2x\,\delta x\),
differential of \(x^3 = 3x^2\,\delta x\),
differential of \(x^4 = 4x^3\,\delta x\).
From these we see that there is a very simple and definite
law by which we can at once find the differential of
any power of \(x\).
Law. — Reduce the power of \(x\) by one, multiply by
\(\delta x\) and place before the whole a coefficient which is the
same number as the power of \(x\) which we are differentiating;
thus, if we differentiate \(x^5\) we get \(5x^4\,\delta x\); also,
if we differentiate \(x^6\) we get \(6x^5\,\delta x\).
I will repeat here that it is necessary for the student
to get a clear conception of what is meant by differentiation;
and I also repeat that in differentiating any
quantity our object is to find out and get the value of
the very small parts of which it is constructed (the rate
of growth). Thus we have seen that a line is constructed
of small lengths \(\delta x\) all placed together; that a
square grows or evolves by placing fine strips one next
the other; that a cube is built up of thin surfaces placed
one over the other; and so on.
Differentiation Similar to Acceleration. — We have just
said that finding the value of the differential, or one of
the smallest particles whose gradual addition to a quantity
makes the quantity, is the same as finding out the
rate of growth, and this is what we understood by the
ordinary term acceleration. Now we can begin to see
concretely just what we are aiming at in the term
differential. The student should stop right here, think
over all that has gone before and weigh each word of
what we are saying with extreme care, for if he understands
that the differentiation of a quantity gives us
the rate of growth or acceleration of that quantity he
has mastered the most important idea, in fact the keynote
idea of all the calculus; I repeat, the keynote idea.
Before going further let us stop for a little illustration.
115
Example. — If a train is running at a constant speed
of ten miles an hour, the speed is constant, unvarying
and therefore has no rate of change, since it does not
change at all. If we call \(x\) the speed of the train, therefore
\(x\) would be a constant quantity, and if we put it in an
equation it would have a constant value and be called a
constant. In algebra we have seen that we do not
usually designate a constant or known quantity by the
symbol \(x\), but rather by the symbols \(a\), \(k\), etc.
Now on the other hand suppose the speed of the train
was changing; say in the first hour it made ten miles, in
the second hour eleven miles, in the third hour twelve
miles, in the fourth hour thirteen miles, etc. It is evident
that the speed is increasing one mile per hour each
hour. This increase of speed we have always called the
acceleration or rate of growth of the speed. Now if we
designated the speed of the train by the symbol \(x\), we
see that \(x\) would be a variable quantity and would have
a different value for every hour, every minute, every
second, every instant that the train was running. The
speed \(x\) would constantly at every instant have added
to it a little more speed, namely \(\delta x\), and if we can find
the value of this small quantity \(\delta x\) for each instant of
time we would have the differential of speed \(x\), or in
other words the acceleration of the speed \(x\). Now let us
repeat, \(x\) would have to be a variable quantity in order
to have any differential at all, and if it is a variable quantity
and has a differential, then that differential is the
rate of growth or acceleration with which the value of
that quantity \(x\) is increasing or diminishing as the case
may be. We now see the significance of the term
differential.
116
One more illustration. We all know that if a ball
is thrown straight up in the air it starts up with great
speed and gradually stops and begins to fall. Then as
it falls it continues to increase its speed of falling until
it strikes the earth with the same speed that it was
thrown up with. Now we know that the force of
gravity has been pulling on that ball from the time that
it left our hands and has accelerated its speed backwards
until it came to a stop in the air, and then
speeded it to the earth. This instantaneous change in
the speed of the ball we have called the acceleration of
gravity, and is the rate of change of the speed of the ball.
From careful observation we find this to be 32 ft. per
second per second. A little further on we will learn
how to express the concrete value of \(\delta x\) in simple
form.
Differentiation of Constants. — Now let us remember
that a constant quantity, since it has no rate of change,
cannot be differentiated; therefore its differential is zero.
If, however, a variable quantity such as \(x\) is multiplied by
a constant quantity such as 6, making the quantity \(6x\),
of course this does not prevent you from differentiating
the variable part, namely \(x\); but of course the constant
quantity remains unchanged; thus the differential of
6 = 0.
117

Fig. 37
119
But the differential of \(3x = 3\,\delta x\),
the differential of \(4x^2 = 4\) times \(2x\,\delta x = 8x\,\delta x\),
the differential of \(2x^3 = 2\) times \(3x^2\,\delta x = 6x^2\,\delta x\), and so on.
Differential of a Sum or Difference. — We have seen
how to find the differential of a single term. Let us now
take up an algebraic expression consisting of several
terms with positive or negative signs before them; for
example
\(x^2 − 2x + 6 + 3x^4\).
In differentiating such an expression it is obvious that
we must differentiate each term separately, for each
term is separate and distinct from the other terms, and
therefore its differential or rate of growth will be distinct
and separate from the differential of the other
terms; thus
118
The differential of \((x^2 − 2x + 6 + 3x^4)\)
= \(2x\,\delta x − 2\,\delta x + 12x^3\,\delta x\).
We need scarcely say that if we differentiate one side
of an algebraic equation we must also differentiate the
other side; for we have already seen that whatever operation
is performed to one side of an equation must be
performed to the other side in order to retain the
equality. Thus if we differentiate
\(x^2 + 4 = 6x − 10\),
we get
\(2x\,\delta x + 0 = 6\,\delta x − 0\),
or
\(2x\,\delta x = 6\,\delta x\).
Differentiation of a Product. — In Fig. 37 we have
a rectangle whose sides are \(x\) and \(y\) and whose area is
therefore equal to the product \(xy\). Now increase its
sides by a small amount and we have the old area
added to by two thin strips and a small rectangle,
thus:
New area = Old area + \(y\,\delta x + \,\delta y\,\delta x + x\,\delta y\).
Fig. 37
\(\delta y \,\delta x\) is negligibly small; therefore we see that the
differential of the original area \(xy = x\,\delta y + y\,\delta x\). This
can be generalized for every case and we have the law
Law. — “The differential of the product of two variables
is equal to the first multiplied by the differential of
the second plus the second multiplied by the differential
of the first.” Thus,
Differential \(x^2y = x^2\,\delta y + 2yx\,\delta x\).
This law holds for any number of variables.
Differential \(xyz = xy\,\delta z + xz\,\delta y + yz\,\delta x\).
Differential of a Fraction. — If we are asked to differentiate
the fraction \(\tfrac{x}{y}\) we first write it in the form \(xy^{-1}\),
using the negative exponent; now on differentiating we
have
Differential \(xy^{-1} = −xy^{-2}\,\delta y + y^{-1}\,\delta x\)
\( = −\frac{x\,\delta y}{y^2} + \frac{\,\delta x}{y}\)
Reducing to a common denominator we have
Differential \(xy^{-1}\) or \(\frac{x}{y} = −\frac{x\,\delta y}{y^2} + \frac{y\,\delta x}{y^2}\)
\( = −\frac{y\,\delta x − x\,\delta y}{y^2}\)120
Law. — The differential of a fraction is then seen to
be equal to the differential of the numerator times the
denominator, minus the differential of the denominator
times the numerator, all divided by the square of the
denominator.
Differential of One Quantity with Respect to Another. —
Thus far we have considered the differential of a
variable with respect to itself, that is, we have considered
its rate of development in so far as it was itself alone
concerned. Suppose however we have two variable
quantities dependent on each other, that is, as one
changes the other changes, and we are asked to find the
rate of change of the one with respect to the other,
that is, to find the rate of change of one knowing the
rate of change of the other. At a glance we see that
this should be a very simple process, for if we know the
relation which subsists between two variable quantities,
this relation being expressed in the form of an equation
between the two quantities, we should readily be able
to tell the relation which will hold between similar
deductions from these quantities. Let us for instance
take the equation
\(x = y + 2\).
Here we have the two variables \(x\) and \(y\) tied together
by an equation which establishes a relation between
them. As we have previously seen, if we give any
definite value to \(y\) we will find a corresponding value
for \(x\). Referring to our chapter on coördinate geometry
we see that this is the equation of the line shown in
Fig. 38.
121

Fig. 38
Fig. 38
Let us take any point \(P\) on this line. Its coördinates
are \(y\) and \(x\) respectively. Now choose another
point \(P{_1}\) a short distance away from \(P\) on the same
line. The abscissa of this new point will be a little
longer than that of the old point, and will equal \(x + \,\delta x\),
while the ordinate \(y\) of the old point has been increased
by \(\delta y\), making the ordinate of the new point \(y + \,\delta y\).
From Fig. 38 we see that
\(tan \alpha = \frac{\,\delta y}{\,\delta x}\).
Therefore, if we know the tangent \(\alpha \) and know either \(\delta y\)
or \(\delta x\) we can find the other.
122

Fig. 39
123
In this example our equation represents a straight
line, but the same would be true for any curve represented
by any equation between \(x\) and \(y\) no matter how
complicated; thus Fig. 39 shows the relation between
\(\delta x\) and \(\delta y\) at one point of the curve (a circle) whose
equation is \(x^2 + y^2 = 25\). For every other point of the
circle \(tan \alpha \) or \(\tfrac{\,\delta y}{\,\delta x}\) will have a different value. \(\delta x\) and
\(\delta y\) while shown quite large in the figure for demonstration’s
sake are inconceivably small in reality; therefore
the line \(AB\) in the figure is really a tangent of the
curve, and \(\measuredangle \alpha \) is the angle which it makes with the
\(x\) axis. For every point on the curve this angle will be
different.
Fig. 39
Mediate Differentiation. — Summarizing the foregoing
we see that if we know any two of the three unknowns
in equation \(tan \alpha = \tfrac{\,\delta y}{\,\delta x}\) we can find the third.
Some textbooks represent \(tan \alpha \) or \(\tfrac{\,\delta y}{\,\delta x}\) by \(yₓ\) and, \(\tfrac{\,\delta x}{\,\delta y} by x_{y}\).
This is a convenient notation and we will use it here.
Therefore we have
\(\delta x tan \alpha = \,\delta y\),
\(\frac{\,\delta y}{tan a} = \,\delta x\),
or
\(\delta y = \,\delta x yₓ\),
\(\delta x = \,\delta y x_{y}\).
This shows us that if we differentiate the quantity
\(3x^2\) as to \(x\) we obtain \(6 x\,\delta x\), but if we had wished to
differentiate it with respect to \(y\) we would first have to
differentiate it with respect to \(x\) and then multiply by
\(x_{y}\), thus:
Differentiation of \(3x^2\) as to \(y = 6 x \,\delta y x_{y}\).
Likewise if we have \(4y^3\) and we wish to differentiate it
with respect to \(x\) we have
Differential of \(4 y^3\) as to \(x = 12 y^2 \,\delta x yₓ\).
This is called mediate differentiation and is resorted to
primarily because we can differentiate a power with
respect to itself readily, but not with respect to some
other variable.
124
Law. — To differentiate any expression containing
\(x\) as to \(y\), first differentiate it as to \(x\) and then multiply
by \(x_{y}\,\delta y\) or vice versa.
We need this principle if we find the differential of
several terms some containing \(x\) and some \(y\); thus if we
differentiate the equation \(2x^2 = y^2 − 10\) with respect
to \(x\) we get
\(4x\,\delta x = 3y^2yₓ\,\delta x + 0\),
or
\(4x = 3y^2yₓ\),
or
\(yₓ = \frac{4x}{3y^2}\),
Therefore
tan \(\alpha = \frac{4x}{3y^2}\).
From this we see that by differentiating the original
equation of the curve we got finally an equation giving
the value \(tan \alpha \) in terms of \(x\) and \(y\), and if we fill out the
exact numerical values of \(x\) and \(y\) for any particular point
of the curve we will immediately be able to determine
the slant of the tangent of the curve at this point, as we
will numerically have the value of tangent \(\alpha \), and a is
the angle that the tangent makes with the \(x\) axis.
125

Fig. 40
127INTEGRATION

Fig. 41
128
In just the same manner that we have proceeded
here we can proceed to find the direction of the tangent
of any curve whose equation we know. The differential
of \(y\) as to \(x\), namely \(\tfrac{\,\delta y}{\,\delta x}\) or \(yₓ\), must be kept in
mind as the rate of change of \(y\) with respect to \(x\), and
nothing so vividly portrays this fact as the inclination
of the tangent to the curve which shows the bend of
the curve at every point.
Differentials of Other Functions. — By elaborate processes
which cannot be mentioned here we find that the
Differential of the sine \(x\) as to \(x =\) cosine \(x \,\delta x\).
Differential of the cosine \(x\) as to \(x =\) − sin \(x\,\delta x\).
Differential of the log \(x\) as to \(x = \frac{1}{x}\,\delta x\).
Differential of the sine \(y\) as to \(x =\) cosine \(yyₓ\,\delta x\).
Differential of the cosine \(y\) as to \(x =\) − sine \(yyₓ\,\delta x\).
Differential of the log \(y\) as to \(x = \frac{1}{y}yₓ\,\delta x\).
Maxima and Minima. — Referring back to the circle,
Fig. 39, once more, we see that
\(x^2 + y^2 = 25\).
Differentiating this equation with reference to \(x\) we
have
\(2x\,\delta x + 2yyₓ\,\delta x = 0\),
or
\(2x + 2yyₓ = 0\),
or
\(yₓ = −\frac{x}{y}\),
Therefore
tan \(\alpha = −\frac{x}{y}\).126
Now when tan \(a = 0\) it is evident that the tangent to
the curve is parallel to the \(x\) axis. At this point \(y\) is
either a maximum or a minimum which can be readily
determined on reference to the curve.
\(0 = \frac{x}{y}\),
\(x = 0\).
Therefore \(x = 0\) when \(y\) is maximum and in this particular
curve also minimum.
Law. — If we want to find the maximum or minimum
value of \(x\) in any equation containing \(x\) and \(y\),
we differentiate the equation with reference to \(y\) and
solve for the value of \(x_{y}\); this we make equal to 0 and
then we solve for the value of \(y\) in the resulting
equation.
Example. — Find the maximum or minimum value
of \(x\) in the equation
\(y^2 = 14x\).
Differentiating with respect to \(y\) we have
\(2y\,\delta y = 14x_{y}\,\delta y\),
\(x_{y} = \frac{2y}{14}\).
\(x_{y} = \frac{2y}{14}\).
Equating this to 0 we have
\(\frac{2y}{14} = 0\),
or
\(y = 0\).
In other words, we find that x has its minimum value
when \(y = 0\). We can readily see that this is actually
the case in Fig. 40, which shows the curve (a parabola).
Fig. 40
Integration is the exact opposite of differentiation.
In differentiation we divide a body into its constituent
parts, in integration we add these constituent parts
together to produce the body.
Integration is indicated by the sign \(∫\); thus, if we
wished to integrate \(\delta x\) we would write
\(∫\,\delta x\)
Since integration is the opposite of differentiation, if we
are given a quantity and asked to integrate it, our
answer would be that quantity which differentiated
will give us our original quantity. For example, we
detect \(\delta x\) as the derivative of \(x\); therefore the integral
\(∫\,\delta x = x\). Likewise, we detect \(4x^3\,\delta x\) as the differential
of \(x^4\) therefore the integral \(∫4x^3\,\delta x = x^4\).
Fig. 41
If we consider the line \(AB\) (Fig. 35) to be made up of
small parts \(\delta x\), we could sum up these parts thus:
\(\delta x + \,\delta x + \,\delta x + \,\delta x + \,\delta x + \,\delta x\) . . . . . .
for millions of parts. But integration enables us to express
this more simply and \(∫\,\delta x\) means the summation
of every single part \(\delta x\) which goes to make up the line
\(AB\), no matter how many parts there may be or how
small each part. But \(x\) is the whole length of the line
of indefinite length. To sum up any portion of the line
between the points or limits \(x = 1\) and \(x = 4\), we
would write
\(\int_{x=1}^{x=4} \,\delta x=(x)_{x=1}^{x=4}\).
129
Now these are definite integrals because they indicate
exactly between what limits or points we wish to find
the length of the line. This is true for all integrals.
Where no limits of integration are shown the integral
will yield only a general result, but when limits are
stated between which summation is to be made, then we
have a definite integral whose precise value we may
ascertain.
Refer back to the expression \(x=(x)_{x=1}^{x=4}\) in order to
solve this, substitute inside of the parenthesis the
value of \(x\) for the upper limit of \(x\), namely, 4, and substitute
and subtract the value of \(x\) at the lower limit,
namely, 1; we then get
\((x)_{x=1}^{x=4} = (4 − 1) = 3\).
Thus 3 is the length of the line between 1 and 4. Or,
to give another illustration, suppose the solution of
some integral had given us
\((x^2 − 1)_{x=2}^{x=3}\),
then
\((x^2 − 1)_{x=2}^{x=3} = (3^2 − 1) − (2^2 − 1) = 5\).
Here we simply substituted for \(x\) in the parenthesis its
upper limit, then subtracted from the quantity thus
obtained another quantity, which is had by substituting
the lower limit of \(x\).
130
By higher mathematics and the theories of series we
prove that the integral of any power of a variable as to
itself is obtained by increasing the exponent by one and
dividing by the new exponent, thus:
\(\int{x^2} \,\delta x=\frac{x^3}{3}\),
\(\int 4 x^5 \,\delta x=\frac{4 x^6}{6}\).
On close inspection this is seen to be the inverse of the
law of differentiation, which says to decrease the exponent
by one and multiply by the old exponent.
So many and so complex are the laws of nature and
so few and so limited the present conceptions of man
that only a few type forms of integrals may be actually
integrated. If the quantity under the integral sign by
some manipulation or device is brought into a form
where it is recognized as the differential of another
quantity, then integrating it will give that quantity.
131
The Integral of an Expression. — The integral of an
algebraic expression consisting of several terms is equal
to the sum of the integrals of each of the separate terms;
thus,
\(\int{x^2} \,\delta x + 2x \,\delta x + 3 \,\delta x\)
is the same thing as
\(\int x^2 \,\delta x + \int 2 x \,\delta x + \int 3 \,\delta x\),
The most common integrals to be met with practically
are:
(1) The integrals of some power of the variable
whose solution we have just explained
(2) The integrals of the sine and cosine, which are
\(\int\) cosine \(x \,\delta x =\) sine \(x\),
\(\int\) sine \(x \,\delta x =\) −cosine \(x\).
(3) The integral of the reciprocal, which is
\(\int \frac{1}{x} \,\delta x=\log{_e}x\).[*]
[*] \(log{_e}\) means natural logarithm or logarithm to the Napierian base \(e\)
which is equal to 2.718 as distinguished from ordinary logarithms to the
base 10. In fact wherever log appears in this chapter it means \(log{_e}\).
Areas. — Up to the present we have considered only
the integration of a quantity with respect to itself.
Suppose now we integrate one quantity with respect to
another.
132

Fig. 42
136LOGARITHMS 100 TO 1000
137LOGARITHMS 100 TO 1000
138NATURAL SINES
139NATURAL SINES
140NATURAL COSINES
141NATURAL COSINES
142NATURAL TANGENTS
143NATURAL TANGENTS
146
147
In Fig. 41 we have the curve \(PP{_1}\), which is the graphical
representation of some equation containing \(x\) and \(y\).
If we wish to find the area which lies between the curve
and the \(x\) axis and between the two vertical lines
drawn at distances \(x = a\) and \(x = b\) respectively, we
divide the space up by vertical lines drawn \(\delta x\) distance
apart. Now we would have a large number of small
strips each \(\delta x\) wide and all having different heights,
namely, \(y{_1}\), \(y{_2}\), \(y{_3}\), \(y{_4}\), etc.
The enumeration of all these areas would then be
\(y{_1} \,\delta x + y{_2} \,\delta x + y{_3} \,\delta x + y{_4} \,\delta x\), etc.
Now calculus enables us to say
Area wanted = \(\int_{x=b}^{x=a} y \,\delta x\).
This integral \(\int_{x=b}^{x=a} y \,\delta x\) cannot be readily solved. If
it were \(\int x \,\delta x\) we have seen that the result would be
\(\tfrac{x^2}{2}\) but this is not the case with \(\int x \,\delta x\). We must then
find some way to replace \(y\) in this integral by some expression
containing \(x\). It is here then that we have to
resort to the equation of the curve \(PP{_1}\) From this
equation we find the value of \(y\) in terms of \(x\); we then
substitute this value of \(y\) in the integral \(\int x \,\delta x\), and then
having an integral of \(x\) as to itself we can readily solve
it. Now, if the equation of the curve \(PP{_1}\) is a complex
one this process becomes very difficult and sometimes
impossible.
A simple case of the above is the hyperbola \(xy = 10\)
(Fig. 42). If we wish to get the value of the shaded
area we have
Shaded area = \(\int_{x=5 ft.}^{x=12 ft.} y \,\delta x\)
From the equation of this curve we have
\(xy = 10\),
\(y = \frac{10}{x}\).
133
Fig. 42
Therefore, substituting we have
Shaded area = \(\int_{x=5}^{x=12} \frac{10}{x} \,\delta x\).
Area = \(10 (\log{_e}x)_{x=5}^{x=12}\)
= \(10 (\log{_e}12) − (\log{_e} 5)\)
= \(10 (2.4817 − 1.6077)\).
Area = 8.740 sq. ft.
Beyond this brief gist of the principles of calculus we
can go no further in this chapter. The student may not
understand the theories herein treated of at first—in
fact, it will take him, as it has taken every student,
many months before the true conceptions of calculus
dawn on him clearly. And, moreover, it is not essential
that he know calculus at all to follow the ordinary
engineering discussions. It is only where a student
wishes to obtain the deepest insight into the science that
he needs calculus, and to such a student I hope this
chapter will be of service as a brief preliminary to the
difficulties and complexities of that subject.
134
135
136
PROBLEMS
1. Differentiate \(2x^3\) as to x.
2. Differentiate \(12x^2\) as to x.
3. Differentiate \(8x^5\) as to x.
4. Differentiate \(3x^2 + 4x + 10 = 5x^2\) as to x.
5. Differentiate \(4y^2 − 3x\) as to \(y\).
6. Differentiate \(14y^4x^3\) as to \(y\).
7. Differentiate \(\frac{x^2}{y}\) as to \(x\).
8. Differentiate \(2y^2 − 4qx\) as to \(y\).
Find \(yₓ\), in the following equations:
9. \(x^2 + 2y^2 = 100\).
10. \(x^3 + y = 5\).
11. \(x^2 − y^2 = 25\).
12. \(5 xy = 12\).
13. What angle does the tangent line to the circle \(x^2 + y^2 = 9\) make with the \(x\) axis at the point where \(x = 2\)?
14. What is the minimum value of \(y\) in the equation \(x^2 = 15y\)?
15. Solve \(∫2x^3 \,\delta x\).
16. Solve \(∫5x^2\,\delta x\).
17. Solve \(∫10ax\,\delta x +5x^2\,\delta x + 3\,\delta x\)
18. Solve \(∫ 3\) sine \(x \,\delta x\).
19. Solve \(∫ 2\) cosine \(x \,\delta x\).
20. Solve \(∫_{x=2}^{x=5} 3 x^2 \,\delta x\).
21. Solve \(∫_{x=2}^{x=18} y \,\delta x\) if \(xy = 4\).
22. Differentiate \(10\) sine \(x\) as to \(x\).
23. Differentiate cosine \(x\) sine \(x\) as to \(x\).
24. Differentiate log \(x\) as to \(x\).
25. Differentiate \(\frac{y^2}{x^2}\) as to \(x\).
The following tables are reproduced from Ames and
Bliss’s “Manual of Experimental Physics” by permission
of the American Book Company.
REFERENCE MATERIAL
Tables of Logarithms and Trigonometry
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 10 | 0000 | 0043 | 0086 | 0128 | 0170 | 0212 | 0253 | 0294 | 0334 | 0374 | Use preceding Table | ||||||||
| 11 | 0414 | 0453 | 0492 | 0531 | 0569 | 0607 | 0645 | 0682 | 0719 | 0755 | 4 | 8 | 11 | 15 | 19 | 23 | 26 | 30 | 34 |
| 12 | 0792 | 0828 | 0864 | 0899 | 0934 | 0969 | 1004 | 1038 | 1072 | 1106 | 3 | 7 | 10 | 14 | 17 | 21 | 24 | 28 | 31 |
| 13 | 1139 | 1173 | 1206 | 1239 | 1271 | 1303 | 1335 | 1367 | 1399 | 1430 | 3 | 6 | 10 | 13 | 16 | 19 | 23 | 26 | 29 |
| 14 | 1461 | 1492 | 1523 | 1553 | 1584 | 1614 | 1644 | 1673 | 1703 | 1732 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 |
| 15 | 1761 | 1790 | 1818 | 1847 | 1875 | 1903 | 1931 | 1959 | 1987 | 2014 | 3 | 6 | 8 | 11 | 14 | 17 | 20 | 22 | 25 |
| 16 | 2041 | 2068 | 2095 | 2122 | 2148 | 2175 | 2201 | 2227 | 2253 | 2279 | 3 | 5 | 8 | 11 | 13 | 16 | 18 | 21 | 24 |
| 17 | 2304 | 2330 | 2355 | 2380 | 2405 | 2430 | 2455 | 2480 | 2504 | 2529 | 2 | 5 | 7 | 10 | 12 | 15 | 17 | 20 | 22 |
| 18 | 2553 | 2577 | 2601 | 2625 | 2648 | 2672 | 2695 | 2718 | 2742 | 2765 | 2 | 5 | 7 | 9 | 12 | 14 | 16 | 19 | 21 |
| 19 | 2788 | 2810 | 2833 | 2856 | 2878 | 2900 | 2923 | 2945 | 2967 | 2989 | 2 | 4 | 7 | 9 | 11 | 13 | 16 | 18 | 20 |
| 20 | 3010 | 3032 | 3054 | 3075 | 3096 | 3118 | 3139 | 3160 | 3181 | 3201 | 2 | 4 | 6 | 8 | 11 | 13 | 15 | 17 | 19 |
| 21 | 3222 | 3243 | 3263 | 3284 | 3304 | 3324 | 3345 | 3365 | 3385 | 3404 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 |
| 22 | 3424 | 3444 | 3464 | 3483 | 3502 | 3522 | 3541 | 3560 | 3579 | 3598 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 15 | 17 |
| 23 | 3617 | 3636 | 3655 | 3674 | 3692 | 3711 | 3729 | 3747 | 3766 | 3784 | 2 | 4 | 6 | 7 | 9 | 11 | 13 | 15 | 17 |
| 24 | 3802 | 3820 | 3838 | 3856 | 3874 | 3892 | 3909 | 3927 | 3945 | 3962 | 2 | 4 | 5 | 7 | 9 | 11 | 12 | 14 | 16 |
| 25 | 3979 | 3997 | 4014 | 4031 | 4048 | 4065 | 4082 | 4099 | 4116 | 4133 | 2 | 3 | 5 | 7 | 9 | 10 | 12 | 14 | 15 |
| 26 | 4150 | 4166 | 4183 | 4200 | 4216 | 4232 | 4249 | 4265 | 4281 | 4298 | 2 | 3 | 5 | 7 | 8 | 10 | 11 | 13 | 15 |
| 27 | 4314 | 4330 | 4346 | 4362 | 4378 | 4393 | 4409 | 4425 | 4440 | 4456 | 2 | 3 | 5 | 6 | 8 | 9 | 11 | 13 | 14 |
| 28 | 4472 | 4487 | 4502 | 4518 | 4533 | 4548 | 4564 | 4579 | 4594 | 4609 | 2 | 3 | 5 | 6 | 8 | 9 | 11 | 12 | 14 |
| 29 | 4624 | 4639 | 4654 | 4669 | 4683 | 4698 | 4713 | 4728 | 4742 | 4757 | 1 | 3 | 4 | 6 | 7 | 9 | 10 | 12 | 13 |
| 30 | 4771 | 4786 | 4800 | 4814 | 4829 | 4843 | 4857 | 4871 | 4886 | 4900 | 1 | 3 | 4 | 6 | 7 | 9 | 10 | 11 | 13 |
| 31 | 4914 | 4928 | 4942 | 4955 | 4969 | 4983 | 4997 | 5011 | 5024 | 5038 | 1 | 3 | 4 | 6 | 7 | 8 | 10 | 11 | 12 |
| 32 | 5051 | 5065 | 5079 | 5092 | 5105 | 5119 | 5132 | 5145 | 5159 | 5172 | 1 | 3 | 4 | 5 | 7 | 8 | 9 | 11 | 12 |
| 33 | 5185 | 5198 | 5211 | 5224 | 5237 | 5250 | 5263 | 5276 | 5289 | 5302 | 1 | 3 | 4 | 5 | 6 | 8 | 9 | 10 | 12 |
| 34 | 5315 | 5328 | 5340 | 5353 | 5366 | 5378 | 5391 | 5403 | 5416 | 5428 | 1 | 3 | 4 | 5 | 6 | 8 | 9 | 10 | 11 |
| 35 | 5441 | 5453 | 5465 | 5478 | 5490 | 5502 | 5514 | 5527 | 5539 | 5551 | 1 | 2 | 4 | 5 | 6 | 7 | 9 | 10 | 11 |
| 36 | 5563 | 5575 | 5587 | 5599 | 5611 | 5623 | 5635 | 5647 | 5658 | 5670 | 1 | 2 | 4 | 5 | 6 | 7 | 8 | 10 | 11 |
| 37 | 5682 | 5694 | 5705 | 5717 | 5729 | 5740 | 5752 | 5763 | 5775 | 5786 | 1 | 2 | 3 | 5 | 6 | 7 | 8 | 9 | 10 |
| 38 | 5798 | 5809 | 5821 | 5832 | 5843 | 5855 | 5866 | 5877 | 5888 | 5899 | 1 | 2 | 3 | 5 | 6 | 7 | 8 | 9 | 10 |
| 39 | 5911 | 5922 | 5933 | 5944 | 5955 | 5966 | 5977 | 5988 | 5999 | 6010 | 1 | 2 | 3 | 4 | 6 | 7 | 8 | 9 | 10 |
| 40 | 6021 | 6031 | 6042 | 6053 | 6064 | 6075 | 6085 | 6096 | 6107 | 6117 | 1 | 2 | 3 | 4 | 5 | 6 | 8 | 9 | 10 |
| 41 | 6128 | 6138 | 6149 | 6160 | 6170 | 6180 | 6191 | 6201 | 6212 | 6222 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 42 | 6232 | 6243 | 6253 | 6263 | 6274 | 6284 | 6294 | 6304 | 6314 | 6325 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 43 | 6335 | 6345 | 6355 | 6365 | 6375 | 6385 | 6395 | 6405 | 6415 | 6425 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 44 | 6435 | 6444 | 6454 | 6464 | 6474 | 6484 | 6493 | 6503 | 6513 | 6522 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 45 | 6532 | 6542 | 6551 | 6561 | 6571 | 6580 | 6590 | 6599 | 6609 | 6618 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 46 | 6628 | 6637 | 6646 | 6656 | 6665 | 6675 | 6684 | 6693 | 6702 | 6712 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 7 | 8 |
| 47 | 6721 | 6730 | 6739 | 6749 | 6758 | 6767 | 6776 | 6785 | 6794 | 6803 | 1 | 2 | 3 | 4 | 5 | 5 | 6 | 7 | 8 |
| 48 | 6812 | 6821 | 6830 | 6839 | 6848 | 6857 | 6866 | 6875 | 6884 | 6893 | 1 | 2 | 3 | 4 | 4 | 5 | 6 | 7 | 8 |
| 49 | 6902 | 6911 | 6920 | 6928 | 6937 | 6946 | 6955 | 6964 | 6972 | 6981 | 1 | 2 | 3 | 4 | 4 | 5 | 6 | 7 | 8 |
| 50 | 6990 | 6998 | 7007 | 7016 | 7024 | 7033 | 7042 | 7050 | 7059 | 7067 | 1 | 2 | 3 | 3 | 4 | 5 | 6 | 7 | 8 |
| 51 | 7076 | 7084 | 7093 | 7101 | 7110 | 7118 | 7126 | 7135 | 7143 | 7152 | 1 | 2 | 3 | 3 | 4 | 5 | 6 | 7 | 8 |
| 52 | 7160 | 7168 | 7177 | 7185 | 7193 | 7202 | 7210 | 7218 | 7226 | 7235 | 1 | 2 | 2 | 3 | 4 | 5 | 6 | 7 | 7 |
| 53 | 7243 | 7251 | 7259 | 7267 | 7275 | 7284 | 7292 | 7300 | 7308 | 7316 | 1 | 2 | 2 | 3 | 4 | 5 | 6 | 6 | 7 |
| 54 | 7324 | 7332 | 7340 | 7348 | 7356 | 7364 | 7372 | 7380 | 7388 | 7396 | 1 | 2 | 2 | 3 | 4 | 5 | 6 | 6 | 7 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 55 | 7404 | 7412 | 7419 | 7427 | 7435 | 7443 | 7451 | 7459 | 7466 | 7474 | 1 | 2 | 2 | 3 | 4 | 5 | 5 | 6 | 7 |
| 56 | 7482 | 7490 | 7497 | 7505 | 7513 | 7520 | 7528 | 7536 | 7543 | 7551 | 1 | 2 | 2 | 3 | 4 | 5 | 5 | 6 | 7 |
| 57 | 7559 | 7566 | 7574 | 7582 | 7589 | 7597 | 7604 | 7612 | 7619 | 7627 | 1 | 2 | 2 | 3 | 4 | 5 | 5 | 6 | 7 |
| 58 | 7634 | 7642 | 7649 | 7657 | 7664 | 7672 | 7679 | 7686 | 7694 | 7701 | 1 | 1 | 2 | 3 | 4 | 4 | 5 | 6 | 7 |
| 59 | 7709 | 7716 | 7723 | 7731 | 7738 | 7745 | 7752 | 7760 | 7767 | 7774 | 1 | 1 | 2 | 3 | 4 | 4 | 5 | 6 | 7 |
| 60 | 7782 | 7789 | 7796 | 7803 | 7810 | 7818 | 7825 | 7832 | 7839 | 7846 | 1 | 1 | 2 | 3 | 4 | 4 | 5 | 6 | 6 |
| 61 | 7853 | 7860 | 7868 | 7875 | 7882 | 7889 | 7896 | 7903 | 7910 | 7917 | 1 | 1 | 2 | 3 | 4 | 4 | 5 | 6 | 6 |
| 62 | 7924 | 7931 | 7938 | 7945 | 7952 | 7959 | 7966 | 7973 | 7980 | 7987 | 1 | 1 | 2 | 3 | 3 | 4 | 5 | 6 | 6 |
| 63 | 7993 | 8000 | 8007 | 8014 | 8021 | 8028 | 8035 | 8041 | 8048 | 8055 | 1 | 1 | 2 | 3 | 3 | 4 | 5 | 5 | 6 |
| 64 | 8062 | 8069 | 8075 | 8082 | 8089 | 8096 | 8102 | 8109 | 8116 | 8122 | 1 | 1 | 2 | 3 | 3 | 4 | 5 | 5 | 6 |
| 65 | 8129 | 8136 | 8142 | 8149 | 8156 | 8162 | 8169 | 8176 | 8182 | 8189 | 1 | 1 | 2 | 3 | 3 | 4 | 5 | 5 | 6 |
| 66 | 8195 | 8202 | 8209 | 8215 | 8222 | 8228 | 8235 | 8241 | 8248 | 8254 | 1 | 1 | 2 | 3 | 3 | 4 | 5 | 5 | 6 |
| 67 | 8261 | 8267 | 8274 | 8280 | 8287 | 8293 | 8299 | 8306 | 8312 | 8319 | 1 | 1 | 2 | 3 | 3 | 4 | 5 | 5 | 6 |
| 68 | 8325 | 8331 | 8338 | 8344 | 8351 | 8357 | 8363 | 8370 | 8376 | 8382 | 1 | 1 | 2 | 3 | 3 | 4 | 4 | 5 | 6 |
| 69 | 8388 | 8395 | 8401 | 8407 | 8414 | 8420 | 8426 | 8432 | 8439 | 8445 | 1 | 1 | 2 | 3 | 3 | 4 | 4 | 5 | 6 |
| 70 | 8451 | 8457 | 8463 | 8470 | 8476 | 8482 | 8488 | 8494 | 8500 | 8506 | 1 | 1 | 2 | 2 | 3 | 4 | 4 | 5 | 6 |
| 71 | 8513 | 8519 | 8525 | 8531 | 8537 | 8543 | 8549 | 8555 | 8561 | 8567 | 1 | 1 | 2 | 2 | 3 | 4 | 4 | 5 | 5 |
| 72 | 8573 | 8579 | 8585 | 8591 | 8597 | 8603 | 8609 | 8615 | 8621 | 8627 | 1 | 1 | 2 | 2 | 3 | 4 | 4 | 5 | 5 |
| 73 | 8633 | 8639 | 8645 | 8651 | 8657 | 8663 | 8669 | 8675 | 8681 | 8686 | 1 | 1 | 2 | 2 | 3 | 4 | 4 | 5 | 5 |
| 74 | 8692 | 8698 | 8704 | 8710 | 8716 | 8722 | 8727 | 8733 | 8739 | 8745 | 1 | 1 | 2 | 2 | 3 | 4 | 4 | 5 | 5 |
| 75 | 8751 | 8756 | 8762 | 8768 | 8774 | 8779 | 8785 | 8791 | 8797 | 8802 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 5 | 5 |
| 76 | 8808 | 8814 | 8820 | 8825 | 8831 | 8837 | 8842 | 8848 | 8854 | 8859 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 5 | 5 |
| 77 | 8865 | 8871 | 8876 | 8882 | 8887 | 8893 | 8899 | 8904 | 8910 | 8915 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 | 5 |
| 78 | 8921 | 8927 | 8932 | 8938 | 8943 | 8949 | 8954 | 8960 | 8965 | 8971 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 | 5 |
| 79 | 8976 | 8982 | 8987 | 8993 | 8998 | 9004 | 9009 | 9015 | 9020 | 9025 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 | 5 |
| 80 | 9031 | 9036 | 9042 | 9047 | 9053 | 9058 | 9063 | 9069 | 9074 | 9079 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 | 5 |
| 81 | 9085 | 9090 | 9096 | 9101 | 9106 | 9112 | 9117 | 9122 | 9128 | 9133 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 | 5 |
| 82 | 9138 | 9143 | 9149 | 9154 | 9159 | 9165 | 9170 | 9175 | 9180 | 9186 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 | 5 |
| 83 | 9191 | 9196 | 9201 | 9206 | 9212 | 9217 | 9222 | 9227 | 9232 | 9238 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 | 5 |
| 84 | 9243 | 9248 | 9253 | 9258 | 9263 | 9269 | 9274 | 9279 | 9284 | 9289 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 | 5 |
| 85 | 9294 | 9299 | 9304 | 9309 | 9315 | 9320 | 9325 | 9330 | 9335 | 9340 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 | 5 |
| 86 | 9345 | 9350 | 9355 | 9360 | 9365 | 9370 | 9375 | 9380 | 9385 | 9390 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 | 5 |
| 87 | 9395 | 9400 | 9405 | 9410 | 9415 | 9420 | 9425 | 9430 | 9435 | 9440 | 0 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 |
| 88 | 9445 | 9450 | 9455 | 9460 | 9465 | 9469 | 9474 | 9479 | 9484 | 9489 | 0 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 |
| 89 | 9494 | 9499 | 9504 | 9509 | 9513 | 9518 | 9523 | 9528 | 9533 | 9538 | 0 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 |
| 90 | 9542 | 9547 | 9552 | 9557 | 9562 | 9566 | 9571 | 9576 | 9581 | 9586 | 0 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 |
| 91 | 9590 | 9595 | 9600 | 9605 | 9609 | 9614 | 9619 | 9624 | 9628 | 9633 | 0 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 |
| 92 | 9638 | 9643 | 9647 | 9652 | 9657 | 9661 | 9666 | 9671 | 9675 | 9680 | 0 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 |
| 93 | 9685 | 9689 | 9694 | 9699 | 9703 | 9708 | 9713 | 9717 | 9722 | 9727 | 0 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 |
| 94 | 9731 | 9736 | 9741 | 9745 | 9750 | 9754 | 9759 | 9763 | 9768 | 9773 | 0 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 |
| 95 | 9777 | 9782 | 9786 | 9791 | 9795 | 9800 | 9805 | 9809 | 9814 | 9818 | 0 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 |
| 96 | 9823 | 9827 | 9832 | 9836 | 9841 | 9845 | 9850 | 9854 | 9859 | 9863 | 0 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 |
| 97 | 9868 | 9872 | 9877 | 9881 | 9886 | 9890 | 9894 | 9899 | 9903 | 9908 | 0 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 |
| 98 | 9912 | 9917 | 9921 | 9926 | 9930 | 9934 | 9939 | 9943 | 9948 | 9952 | 0 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 |
| 99 | 9956 | 9961 | 9965 | 9969 | 9974 | 9978 | 9983 | 9987 | 9991 | 9996 | 0 | 1 | 1 | 2 | 2 | 3 | 3 | 3 | 4 |
| 0' | 6' | 12' | 18' | 24' | 30' | 36' | 42' | 48' | 54' | 1 | 2 | 3 | 4 | 5 | |
| 0° | 0000 | 0017 | 0035 | 0052 | 0070 | 0087 | 0105 | 0122 | 0140 | 0157 | 3 | 6 | 9 | 12 | 15 |
| 1° | 0175 | 0192 | 0209 | 0227 | 0244 | 0262 | 0279 | 0297 | 0314 | 0332 | 3 | 6 | 9 | 12 | 15 |
| 2° | 0349 | 0366 | 0384 | 0401 | 0419 | 0436 | 0454 | 0471 | 0488 | 0506 | 3 | 6 | 9 | 12 | 15 |
| 3° | 0523 | 0541 | 0558 | 0576 | 0593 | 0610 | 0628 | 0645 | 0663 | 0680 | 3 | 6 | 9 | 12 | 15 |
| 4° | 0698 | 0715 | 0732 | 0750 | 0767 | 0785 | 0802 | 0819 | 0837 | 0854 | 3 | 6 | 9 | 12 | 15 |
| 5° | 0872 | 0889 | 0906 | 0924 | 0941 | 0958 | 0976 | 0993 | 1011 | 1028 | 3 | 6 | 9 | 12 | 14 |
| 6° | 1045 | 1063 | 1080 | 1097 | 1115 | 1132 | 1149 | 1167 | 1184 | 1201 | 3 | 6 | 9 | 12 | 14 |
| 7° | 1219 | 1236 | 1253 | 1271 | 1288 | 1305 | 1323 | 1340 | 1357 | 1374 | 3 | 6 | 9 | 12 | 14 |
| 8° | 1392 | 1409 | 1426 | 1444 | 1461 | 1478 | 1495 | 1513 | 1530 | 1547 | 3 | 6 | 9 | 12 | 14 |
| 9° | 1564 | 1582 | 1599 | 1616 | 1633 | 1650 | 1668 | 1685 | 1702 | 1719 | 3 | 6 | 9 | 11 | 14 |
| 10° | 1736 | 1754 | 1771 | 1788 | 1805 | 1822 | 1840 | 1857 | 1874 | 1891 | 3 | 6 | 9 | 11 | 14 |
| 11° | 1908 | 1925 | 1942 | 1959 | 1977 | 1994 | 2011 | 2028 | 2045 | 2062 | 3 | 6 | 9 | 11 | 14 |
| 12° | 2079 | 2096 | 2113 | 2130 | 2147 | 2164 | 2181 | 2198 | 2215 | 2233 | 3 | 6 | 9 | 11 | 14 |
| 13° | 2250 | 2267 | 2284 | 2300 | 2317 | 2334 | 2351 | 2368 | 2385 | 2402 | 3 | 6 | 9 | 11 | 14 |
| 14° | 2419 | 2436 | 2453 | 2470 | 2487 | 2504 | 2521 | 2538 | 2554 | 2571 | 3 | 6 | 8 | 11 | 14 |
| 15° | 2588 | 2605 | 2622 | 2639 | 2656 | 2672 | 2689 | 2706 | 2723 | 2740 | 3 | 6 | 8 | 11 | 14 |
| 16° | 2756 | 2773 | 2790 | 2807 | 2823 | 2840 | 2857 | 2874 | 2890 | 2907 | 3 | 6 | 8 | 11 | 14 |
| 17° | 2924 | 2940 | 2957 | 2974 | 2990 | 3007 | 3024 | 3040 | 3057 | 3074 | 3 | 6 | 8 | 11 | 14 |
| 18° | 3090 | 3107 | 3123 | 3140 | 3156 | 3173 | 3190 | 3206 | 3223 | 3239 | 3 | 6 | 8 | 11 | 14 |
| 19° | 3256 | 3272 | 3289 | 3305 | 3322 | 3338 | 3355 | 3371 | 3387 | 3404 | 3 | 5 | 8 | 11 | 14 |
| 20° | 3420 | 3437 | 3453 | 3469 | 3486 | 3502 | 3518 | 3535 | 3551 | 3567 | 3 | 5 | 8 | 11 | 14 |
| 21° | 3584 | 3600 | 3616 | 3633 | 3649 | 3665 | 3681 | 3697 | 3714 | 3730 | 3 | 5 | 8 | 11 | 14 |
| 22° | 3746 | 3762 | 3778 | 3795 | 3811 | 3827 | 3843 | 3859 | 3875 | 3891 | 3 | 5 | 8 | 11 | 13 |
| 23° | 3907 | 3923 | 3939 | 3955 | 3971 | 3987 | 4003 | 4019 | 4035 | 4051 | 3 | 5 | 8 | 11 | 13 |
| 24° | 4067 | 4083 | 4099 | 4115 | 4131 | 4147 | 4163 | 4179 | 4195 | 4210 | 3 | 5 | 8 | 11 | 13 |
| 25° | 4226 | 4242 | 4258 | 4274 | 4289 | 4305 | 4321 | 4337 | 4352 | 4368 | 3 | 5 | 8 | 11 | 13 |
| 26° | 4384 | 4399 | 4415 | 4431 | 4446 | 4462 | 4478 | 4493 | 4509 | 4524 | 3 | 5 | 8 | 10 | 13 |
| 27° | 4540 | 4555 | 4571 | 4586 | 4602 | 4617 | 4633 | 4648 | 4664 | 4679 | 3 | 5 | 8 | 10 | 13 |
| 28° | 4695 | 4710 | 4726 | 4741 | 4756 | 4772 | 4787 | 4802 | 4818 | 4833 | 3 | 5 | 8 | 10 | 13 |
| 29° | 4848 | 4863 | 4879 | 4894 | 4909 | 4924 | 4939 | 4955 | 4970 | 4985 | 3 | 5 | 8 | 10 | 13 |
| 30° | 5000 | 5015 | 5030 | 5045 | 5060 | 5075 | 5090 | 5105 | 5120 | 5135 | 3 | 5 | 8 | 10 | 13 |
| 31° | 5150 | 5165 | 5180 | 5195 | 5210 | 5225 | 5240 | 5255 | 5270 | 5284 | 2 | 5 | 7 | 10 | 12 |
| 32° | 5299 | 5314 | 5329 | 5344 | 5358 | 5373 | 5388 | 5402 | 5417 | 5432 | 2 | 5 | 7 | 10 | 12 |
| 33° | 5446 | 5461 | 5476 | 5490 | 5505 | 5519 | 5534 | 5548 | 5563 | 5577 | 2 | 5 | 7 | 10 | 12 |
| 34° | 5592 | 5606 | 5621 | 5635 | 5650 | 5664 | 5678 | 5693 | 5707 | 5721 | 2 | 5 | 7 | 10 | 12 |
| 35° | 5736 | 5750 | 5764 | 5779 | 5793 | 5807 | 5821 | 5835 | 5850 | 5864 | 2 | 5 | 7 | 10 | 12 |
| 36° | 5878 | 5892 | 5906 | 5920 | 5934 | 5948 | 5962 | 5976 | 5990 | 6004 | 2 | 5 | 7 | 9 | 12 |
| 37° | 6018 | 6032 | 6046 | 6060 | 6074 | 6088 | 6101 | 6115 | 6129 | 6143 | 2 | 5 | 7 | 9 | 12 |
| 38° | 6157 | 6170 | 6184 | 6198 | 6211 | 6225 | 6239 | 6252 | 6266 | 6280 | 2 | 5 | 7 | 9 | 11 |
| 39° | 6293 | 6307 | 6320 | 6334 | 6347 | 6361 | 6374 | 6388 | 6401 | 6414 | 2 | 5 | 7 | 9 | 11 |
| 40° | 6428 | 6441 | 6455 | 6468 | 6481 | 6494 | 6508 | 6521 | 6534 | 6547 | 2 | 4 | 7 | 9 | 11 |
| 41° | 6561 | 6574 | 6587 | 6600 | 6613 | 6626 | 6639 | 6652 | 6665 | 6678 | 2 | 4 | 7 | 9 | 11 |
| 42° | 6691 | 6704 | 6717 | 6730 | 6743 | 6756 | 6769 | 6782 | 6794 | 6807 | 2 | 4 | 6 | 9 | 11 |
| 43° | 6820 | 6833 | 6845 | 6858 | 6871 | 6884 | 6896 | 6909 | 6921 | 6934 | 2 | 4 | 6 | 9 | 11 |
| 44° | 6947 | 6959 | 6972 | 6984 | 6997 | 7009 | 7022 | 7034 | 7046 | 7059 | 2 | 4 | 6 | 8 | 10 |
| 0' | 6' | 12' | 18' | 24' | 30' | 36' | 42' | 48' | 54' | 1 | 2 | 3 | 4 | 5 | |
| 45° | 7071 | 7083 | 7096 | 7108 | 7120 | 7133 | 7145 | 7157 | 7169 | 7181 | 2 | 4 | 6 | 8 | 10 |
| 46° | 7193 | 7206 | 7218 | 7230 | 7242 | 7254 | 7266 | 7278 | 7290 | 7302 | 2 | 4 | 6 | 8 | 10 |
| 47° | 7314 | 7325 | 7337 | 7349 | 7361 | 7373 | 7385 | 7396 | 7408 | 7420 | 2 | 4 | 6 | 8 | 10 |
| 48° | 7431 | 7443 | 7455 | 7466 | 7478 | 7490 | 7501 | 7513 | 7524 | 7536 | 2 | 4 | 6 | 8 | 10 |
| 49° | 7547 | 7559 | 7570 | 7581 | 7593 | 7604 | 7615 | 7627 | 7638 | 7649 | 2 | 4 | 6 | 8 | 10 |
| 50° | 7660 | 7672 | 7683 | 7694 | 7705 | 7716 | 7727 | 7738 | 7749 | 7760 | 2 | 4 | 6 | 7 | 9 |
| 51° | 7771 | 7782 | 7793 | 7804 | 7815 | 7826 | 7837 | 7848 | 7859 | 7869 | 2 | 4 | 5 | 7 | 9 |
| 52° | 7880 | 7891 | 7902 | 7912 | 7923 | 7934 | 7944 | 7955 | 7965 | 7976 | 2 | 4 | 5 | 7 | 9 |
| 53° | 7986 | 7997 | 8007 | 8018 | 8028 | 8039 | 8049 | 8059 | 8070 | 8080 | 2 | 3 | 5 | 7 | 9 |
| 54° | 8090 | 8100 | 8111 | 8121 | 8131 | 8141 | 8151 | 8161 | 8171 | 8181 | 2 | 3 | 5 | 7 | 9 |
| 55° | 8192 | 8202 | 8211 | 8221 | 8231 | 8241 | 8251 | 8261 | 8271 | 8281 | 2 | 3 | 5 | 7 | 8 |
| 56° | 8290 | 8300 | 8310 | 8320 | 8329 | 8339 | 8348 | 8358 | 8368 | 8377 | 2 | 3 | 5 | 6 | 8 |
| 57° | 8387 | 8396 | 8406 | 8415 | 8425 | 8434 | 8443 | 8453 | 8462 | 8471 | 2 | 3 | 5 | 6 | 8 |
| 58° | 8480 | 8490 | 8499 | 8508 | 8517 | 8526 | 8536 | 8545 | 8554 | 8563 | 2 | 3 | 5 | 6 | 8 |
| 59° | 8572 | 8581 | 8590 | 8599 | 8607 | 8616 | 8625 | 8634 | 8643 | 8652 | 1 | 3 | 4 | 6 | 7 |
| 60° | 8660 | 8669 | 8678 | 8686 | 8695 | 8704 | 8712 | 8721 | 8729 | 8738 | 1 | 3 | 4 | 6 | 7 |
| 61° | 8746 | 8755 | 8763 | 8771 | 8780 | 8788 | 8796 | 8805 | 8813 | 8821 | 1 | 3 | 4 | 6 | 7 |
| 62° | 8829 | 8838 | 8846 | 8854 | 8862 | 8870 | 8878 | 8886 | 8894 | 8902 | 1 | 3 | 4 | 5 | 7 |
| 63° | 8910 | 8918 | 8926 | 8934 | 8942 | 8949 | 8957 | 8965 | 8973 | 8980 | 1 | 3 | 4 | 5 | 7 |
| 64° | 8988 | 8996 | 9003 | 9011 | 9018 | 9026 | 9033 | 9041 | 9048 | 9056 | 1 | 3 | 4 | 5 | 6 |
| 65° | 9063 | 9070 | 9078 | 9085 | 9092 | 9100 | 9107 | 9114 | 9121 | 9128 | 1 | 2 | 4 | 5 | 6 |
| 66° | 9135 | 9143 | 9150 | 9157 | 9164 | 9171 | 9178 | 9184 | 9191 | 9198 | 1 | 2 | 4 | 5 | 6 |
| 67° | 9205 | 9212 | 9219 | 9225 | 9232 | 9239 | 9245 | 9252 | 9259 | 9265 | 1 | 2 | 3 | 5 | 6 |
| 68° | 9272 | 9278 | 9285 | 9291 | 9298 | 9304 | 9311 | 9317 | 9323 | 9330 | 1 | 2 | 3 | 4 | 5 |
| 69° | 9336 | 9342 | 9348 | 9354 | 9361 | 9367 | 9373 | 9379 | 9385 | 9391 | 1 | 2 | 3 | 4 | 5 |
| 70° | 9397 | 9403 | 9409 | 9415 | 9421 | 9426 | 9432 | 9438 | 9444 | 9449 | 1 | 2 | 3 | 4 | 5 |
| 71° | 9455 | 9461 | 9466 | 9472 | 9478 | 9483 | 9489 | 9494 | 9500 | 9505 | 1 | 2 | 3 | 4 | 5 |
| 72° | 9511 | 9516 | 9521 | 9527 | 9532 | 9537 | 9542 | 9548 | 9553 | 9558 | 1 | 2 | 3 | 4 | 4 |
| 73° | 9563 | 9568 | 9573 | 9578 | 9583 | 9588 | 9593 | 9598 | 9603 | 9608 | 1 | 2 | 3 | 3 | 4 |
| 74° | 9613 | 9617 | 9622 | 9627 | 9632 | 9636 | 9641 | 9646 | 9650 | 9655 | 1 | 2 | 2 | 3 | 4 |
| 75° | 9659 | 9664 | 9668 | 9673 | 9677 | 9681 | 9686 | 9690 | 9694 | 9699 | 1 | 2 | 2 | 3 | 4 |
| 76° | 9703 | 9707 | 9711 | 9715 | 9720 | 9724 | 9728 | 9732 | 9736 | 9740 | 1 | 1 | 2 | 3 | 4 |
| 77° | 9744 | 9748 | 9751 | 9755 | 9759 | 9763 | 9767 | 9770 | 9774 | 9778 | 1 | 1 | 2 | 3 | 3 |
| 78° | 9781 | 9785 | 9789 | 9792 | 9796 | 9799 | 9803 | 9806 | 9810 | 9813 | 1 | 1 | 2 | 2 | 3 |
| 79° | 9816 | 9820 | 9823 | 9826 | 9829 | 9833 | 9836 | 9839 | 9842 | 9845 | 1 | 1 | 2 | 2 | 3 |
| 80° | 9848 | 9851 | 9854 | 9857 | 9860 | 9863 | 9866 | 9869 | 9871 | 9874 | 1 | 1 | 2 | 2 | 3 |
| 81° | 9877 | 9880 | 9882 | 9885 | 9888 | 9890 | 9893 | 9895 | 9898 | 9900 | 0 | 1 | 1 | 2 | 2 |
| 82° | 9903 | 9905 | 9907 | 9910 | 9912 | 9914 | 9917 | 9919 | 9921 | 9923 | 0 | 1 | 1 | 2 | 2 |
| 83° | 9925 | 9928 | 9930 | 9932 | 9934 | 9936 | 9938 | 9940 | 9942 | 9943 | 0 | 1 | 1 | 1 | 2 |
| 84° | 9945 | 9947 | 9949 | 9951 | 9952 | 9954 | 9956 | 9957 | 9959 | 9960 | 0 | 1 | 1 | 1 | 2 |
| 85° | 9962 | 9963 | 9965 | 9966 | 9968 | 9969 | 9971 | 9972 | 9973 | 9974 | 0 | 1 | 1 | 1 | 1 |
| 86° | 9976 | 9977 | 9978 | 9979 | 9980 | 9981 | 9982 | 9983 | 9984 | 9985 | 0 | 0 | 1 | 1 | 1 |
| 87° | 9986 | 9987 | 9988 | 9989 | 9990 | 9990 | 9991 | 9992 | 9993 | 9993 | 0 | 0 | 0 | 1 | 1 |
| 88° | 9994 | 9995 | 9995 | 9996 | 9996 | 9997 | 9997 | 9997 | 9998 | 9998 | 0 | 0 | 0 | 0 | 0 |
| 89° | 9998 | 9999 | 9999 | 9999 | 9999 | 1,000 nearly | 1,000 nearly | 1,000 nearly | 1,000 nearly | 1,000 nearly | 0 | 0 | 0 | 0 | 0 |
| 0' | 6' | 12' | 18' | 24' | 30' | 36' | 42' | 48' | 54' | 1 | 2 | 3 | 4 | 5 | |
| 0° | 1,000 | 1,000 nearly | 1,000 nearly | 1,000 nearly | 1,000 nearly | 0000 | 9999 | 9999 | 9999 | 9999 | 0 | 0 | 0 | 0 | 0 |
| 1° | 9998 | 9998 | 9998 | 9997 | 9997 | 9997 | 9996 | 9996 | 9995 | 9995 | 0 | 0 | 0 | 0 | 0 |
| 2° | 9994 | 9993 | 9993 | 9992 | 9991 | 9990 | 9990 | 9989 | 9988 | 9987 | 0 | 0 | 0 | 0 | 1 |
| 3° | 9986 | 9985 | 9984 | 9983 | 9982 | 9981 | 9980 | 9979 | 9978 | 9977 | 0 | 0 | 0 | 1 | 1 |
| 4° | 9976 | 9974 | 9973 | 9972 | 9971 | 9969 | 9968 | 9966 | 9965 | 9963 | 0 | 0 | 1 | 1 | 1 |
| 5° | 9962 | 9960 | 9959 | 9957 | 9956 | 9954 | 9952 | 9951 | 9949 | 9947 | 0 | 1 | 1 | 1 | 1 |
| 6° | 9945 | 9943 | 9942 | 9940 | 9938 | 9936 | 9934 | 9932 | 9930 | 9928 | 0 | 1 | 1 | 1 | 2 |
| 7° | 9925 | 9923 | 9921 | 9919 | 9917 | 9914 | 9912 | 9910 | 9907 | 9905 | 0 | 1 | 1 | 1 | 2 |
| 8° | 9903 | 9900 | 9898 | 9895 | 9893 | 9890 | 9888 | 9885 | 9882 | 9880 | 0 | 1 | 1 | 2 | 2 |
| 9° | 9877 | 9874 | 9871 | 9869 | 9866 | 9863 | 9860 | 9857 | 9854 | 9851 | 0 | 1 | 1 | 2 | 2 |
| 10° | 9848 | 9845 | 9842 | 9839 | 9836 | 9833 | 9829 | 9826 | 9823 | 9820 | 1 | 1 | 2 | 2 | 3 |
| 11° | 9816 | 9813 | 9810 | 9806 | 9803 | 9799 | 9796 | 9792 | 9789 | 9785 | 1 | 1 | 2 | 2 | 3 |
| 12° | 9781 | 9778 | 9774 | 9770 | 9767 | 9763 | 9759 | 9755 | 9751 | 9748 | 1 | 1 | 2 | 2 | 3 |
| 13° | 9744 | 9740 | 9736 | 9732 | 9728 | 9724 | 9720 | 9715 | 9711 | 9707 | 1 | 1 | 2 | 3 | 3 |
| 14° | 9703 | 9699 | 9694 | 9690 | 9686 | 9681 | 9677 | 9673 | 9668 | 9664 | 1 | 1 | 2 | 3 | 4 |
| 15° | 9659 | 9655 | 9650 | 9646 | 9641 | 9636 | 9632 | 9627 | 9622 | 9617 | 1 | 2 | 2 | 3 | 4 |
| 16° | 9613 | 9608 | 9603 | 9598 | 9593 | 9588 | 9583 | 9578 | 9573 | 9568 | 1 | 2 | 2 | 3 | 4 |
| 17° | 9563 | 9558 | 9553 | 9548 | 9542 | 9537 | 9532 | 9527 | 9521 | 9516 | 1 | 2 | 3 | 3 | 4 |
| 18° | 9511 | 9505 | 9500 | 9494 | 9489 | 9483 | 9478 | 9472 | 9466 | 9461 | 1 | 2 | 3 | 4 | 5 |
| 19° | 9455 | 9449 | 9444 | 9438 | 9432 | 9426 | 9421 | 9415 | 9409 | 9403 | 1 | 2 | 3 | 4 | 5 |
| 20° | 9397 | 9391 | 9385 | 9379 | 9373 | 9367 | 9361 | 9354 | 9348 | 9342 | 1 | 2 | 3 | 4 | 5 |
| 21° | 9336 | 9330 | 9323 | 9317 | 9311 | 9304 | 9298 | 9291 | 9285 | 9278 | 1 | 2 | 3 | 4 | 5 |
| 22° | 9272 | 9265 | 9259 | 9252 | 9245 | 9239 | 9232 | 9225 | 9219 | 9212 | 1 | 2 | 3 | 4 | 5 |
| 23° | 9205 | 9198 | 9191 | 9184 | 9178 | 9171 | 9164 | 9157 | 9150 | 9143 | 1 | 2 | 3 | 5 | 6 |
| 24° | 9135 | 9128 | 9121 | 9114 | 9107 | 9100 | 9092 | 9085 | 9078 | 9070 | 1 | 2 | 4 | 5 | 6 |
| 25° | 9063 | 9056 | 9048 | 9041 | 9033 | 9026 | 9018 | 9011 | 9003 | 8996 | 1 | 2 | 4 | 5 | 6 |
| 26° | 8988 | 8980 | 8973 | 8965 | 8957 | 8949 | 8942 | 8934 | 8926 | 8918 | 1 | 3 | 4 | 5 | 6 |
| 27° | 8910 | 8902 | 8894 | 8886 | 8878 | 8870 | 8862 | 8854 | 8846 | 8838 | 1 | 3 | 4 | 5 | 7 |
| 28° | 8829 | 8821 | 8813 | 8805 | 8796 | 8788 | 8780 | 8771 | 8763 | 8755 | 1 | 3 | 4 | 5 | 7 |
| 29° | 8746 | 8738 | 8729 | 8721 | 8712 | 8704 | 8695 | 8686 | 8678 | 8669 | 1 | 3 | 4 | 6 | 7 |
| 30° | 8660 | 8652 | 8643 | 8634 | 8625 | 8616 | 8607 | 8599 | 8590 | 8581 | 1 | 3 | 4 | 6 | 7 |
| 31° | 8572 | 8563 | 8554 | 8545 | 8536 | 8526 | 8517 | 8508 | 8499 | 8490 | 2 | 3 | 5 | 6 | 8 |
| 32° | 8480 | 8471 | 8462 | 8453 | 8443 | 8434 | 8425 | 8415 | 8406 | 8396 | 2 | 3 | 5 | 6 | 8 |
| 33° | 8387 | 8377 | 8368 | 8358 | 8348 | 8339 | 8329 | 8320 | 8310 | 8300 | 2 | 3 | 5 | 6 | 8 |
| 34° | 8290 | 8281 | 8271 | 8261 | 8251 | 8241 | 8231 | 8221 | 8211 | 8202 | 2 | 3 | 5 | 7 | 8 |
| 35° | 8192 | 8181 | 8171 | 8161 | 8151 | 8141 | 8131 | 8121 | 8111 | 8100 | 2 | 3 | 5 | 7 | 8 |
| 36° | 8090 | 8080 | 8070 | 8059 | 8049 | 8039 | 8028 | 8018 | 8007 | 7997 | 2 | 3 | 5 | 7 | 9 |
| 37° | 7986 | 7976 | 7965 | 7955 | 7944 | 7934 | 7923 | 7912 | 7902 | 7891 | 2 | 4 | 5 | 7 | 9 |
| 38° | 7880 | 7869 | 7859 | 7848 | 7837 | 7826 | 7815 | 7804 | 7793 | 7782 | 2 | 4 | 5 | 7 | 9 |
| 39° | 7771 | 7760 | 7749 | 7738 | 7727 | 7716 | 7705 | 7694 | 7683 | 7672 | 2 | 4 | 5 | 7 | 9 |
| 40° | 7660 | 7649 | 7638 | 7627 | 7615 | 7604 | 7593 | 7581 | 7570 | 7559 | 2 | 4 | 6 | 7 | 9 |
| 41° | 7547 | 7536 | 7524 | 7513 | 7501 | 7490 | 7478 | 7466 | 7455 | 7443 | 2 | 4 | 6 | 8 | 10 |
| 42° | 7431 | 7420 | 7408 | 7396 | 7385 | 7373 | 7361 | 7349 | 7337 | 7325 | 2 | 4 | 6 | 8 | 10 |
| 43° | 7314 | 7302 | 7290 | 7278 | 7266 | 7254 | 7242 | 7230 | 7218 | 7206 | 2 | 4 | 6 | 8 | 10 |
| 44° | 7193 | 7181 | 7169 | 7157 | 7145 | 7133 | 7120 | 7108 | 7096 | 7083 | 2 | 4 | 6 | 8 | 10 |
N.B. - Numbers in difference column to be subtracted, not added.
| 0' | 6' | 12' | 18' | 24' | 30' | 36' | 42' | 48' | 54' | 1 | 2 | 3 | 4 | 5 | |
| 45° | 7071 | 7059 | 7046 | 7034 | 7022 | 7009 | 6997 | 6984 | 6972 | 6959 | 2 | 4 | 6 | 8 | 10 |
| 46° | 6947 | 6934 | 6921 | 6909 | 6896 | 6884 | 6871 | 6858 | 6845 | 6833 | 2 | 4 | 6 | 8 | 10 |
| 47° | 6820 | 6807 | 6794 | 6782 | 6769 | 6756 | 6743 | 6730 | 6717 | 6704 | 2 | 4 | 6 | 9 | 11 |
| 48° | 6691 | 6678 | 6665 | 6652 | 6639 | 6626 | 6613 | 6600 | 6587 | 6574 | 2 | 4 | 6 | 9 | 11 |
| 49° | 6561 | 6547 | 6534 | 6521 | 6508 | 6494 | 6481 | 6468 | 6455 | 6441 | 2 | 4 | 7 | 9 | 11 |
| 50° | 6428 | 6414 | 6401 | 6388 | 6374 | 6361 | 6347 | 6334 | 6320 | 6307 | 2 | 4 | 7 | 9 | 11 |
| 51° | 6293 | 6280 | 6266 | 6252 | 6239 | 6225 | 6211 | 6198 | 6184 | 6170 | 2 | 5 | 7 | 9 | 11 |
| 52° | 6157 | 6143 | 6129 | 6115 | 6101 | 6088 | 6074 | 6060 | 6046 | 6032 | 2 | 5 | 7 | 9 | 11 |
| 53° | 6018 | 6004 | 5990 | 5976 | 5962 | 5948 | 5934 | 5920 | 5906 | 5892 | 2 | 5 | 7 | 9 | 12 |
| 54° | 5878 | 5864 | 5850 | 5835 | 5821 | 5807 | 5793 | 5779 | 5764 | 5750 | 2 | 5 | 7 | 9 | 12 |
| 55° | 5736 | 5721 | 5707 | 5693 | 5678 | 5664 | 5650 | 5635 | 5621 | 5606 | 2 | 5 | 7 | 10 | 12 |
| 56° | 5592 | 5577 | 5563 | 5548 | 5534 | 5519 | 5505 | 5490 | 5476 | 5461 | 2 | 5 | 7 | 10 | 12 |
| 57° | 5446 | 5432 | 5417 | 5402 | 5388 | 5373 | 5358 | 5344 | 5329 | 5314 | 2 | 5 | 7 | 10 | 12 |
| 58° | 5299 | 5284 | 5270 | 5255 | 5240 | 5225 | 5210 | 5195 | 5180 | 5165 | 2 | 5 | 7 | 10 | 12 |
| 59° | 5150 | 5135 | 5120 | 5105 | 5090 | 5075 | 5060 | 5045 | 5030 | 5015 | 2 | 5 | 7 | 10 | 12 |
| 60° | 5000 | 4985 | 4970 | 4955 | 4939 | 4924 | 4909 | 4894 | 4879 | 4863 | 3 | 5 | 8 | 10 | 13 |
| 61° | 4848 | 4833 | 4818 | 4802 | 4787 | 4772 | 4756 | 4741 | 4726 | 4710 | 3 | 5 | 8 | 10 | 13 |
| 62° | 4695 | 4679 | 4664 | 4648 | 4633 | 4617 | 4602 | 4586 | 4571 | 4555 | 3 | 5 | 8 | 10 | 13 |
| 63° | 4540 | 4524 | 4509 | 4493 | 4478 | 4462 | 4446 | 4431 | 4415 | 4399 | 3 | 5 | 8 | 10 | 13 |
| 64° | 4384 | 4368 | 4352 | 4337 | 4321 | 4305 | 4289 | 4274 | 4258 | 4242 | 3 | 5 | 8 | 10 | 13 |
| 65° | 4226 | 4210 | 4195 | 4179 | 4163 | 4147 | 4131 | 4115 | 4099 | 4083 | 3 | 5 | 8 | 11 | 13 |
| 66° | 4067 | 4051 | 4035 | 4019 | 4003 | 3987 | 3971 | 3955 | 3939 | 3923 | 3 | 5 | 8 | 11 | 13 |
| 67° | 3907 | 3891 | 3875 | 3859 | 3843 | 3827 | 3811 | 3795 | 3778 | 3762 | 3 | 5 | 8 | 11 | 13 |
| 68° | 3746 | 3730 | 3714 | 3697 | 3681 | 3665 | 3649 | 3633 | 3616 | 3600 | 3 | 5 | 8 | 11 | 13 |
| 69° | 3584 | 3567 | 3551 | 3535 | 3518 | 3502 | 3486 | 3469 | 3453 | 3437 | 3 | 5 | 8 | 11 | 14 |
| 70° | 3420 | 3404 | 3387 | 3371 | 3355 | 3338 | 3322 | 3305 | 3289 | 3272 | 3 | 5 | 8 | 11 | 14 |
| 71° | 3256 | 3239 | 3223 | 3206 | 3190 | 3173 | 3156 | 3140 | 3123 | 3107 | 3 | 6 | 8 | 11 | 14 |
| 72° | 3090 | 3074 | 3057 | 3040 | 3024 | 3007 | 2990 | 2974 | 2957 | 2940 | 3 | 6 | 8 | 11 | 14 |
| 73° | 2924 | 2907 | 2890 | 2874 | 2857 | 2840 | 2823 | 2807 | 2790 | 2773 | 3 | 6 | 8 | 11 | 14 |
| 74° | 2756 | 2740 | 2723 | 2706 | 2689 | 2672 | 2656 | 2639 | 2622 | 2605 | 3 | 6 | 8 | 11 | 14 |
| 75° | 2588 | 2571 | 2554 | 2538 | 2521 | 2504 | 2487 | 2470 | 2453 | 2436 | 3 | 6 | 8 | 11 | 14 |
| 76° | 2419 | 2402 | 2385 | 2368 | 2351 | 2334 | 2317 | 2300 | 2284 | 2267 | 3 | 6 | 8 | 11 | 14 |
| 77° | 2250 | 2233 | 2215 | 2198 | 2181 | 2164 | 2147 | 2130 | 2113 | 2096 | 3 | 6 | 9 | 11 | 14 |
| 78° | 2079 | 2062 | 2045 | 2028 | 2011 | 1994 | 1977 | 1959 | 1942 | 1925 | 3 | 6 | 9 | 11 | 14 |
| 79° | 1908 | 1891 | 1874 | 1857 | 1840 | 1822 | 1805 | 1788 | 1771 | 1754 | 3 | 6 | 9 | 11 | 14 |
| 80° | 1736 | 1719 | 1702 | 1685 | 1668 | 1650 | 1633 | 1616 | 1599 | 1582 | 3 | 6 | 9 | 11 | 14 |
| 81° | 1564 | 1547 | 1530 | 1513 | 1495 | 1478 | 1461 | 1444 | 1426 | 1409 | 3 | 6 | 9 | 11 | 14 |
| 82° | 1392 | 1374 | 1357 | 1340 | 1323 | 1305 | 1288 | 1271 | 1253 | 1236 | 3 | 6 | 9 | 12 | 14 |
| 83° | 1219 | 1201 | 1184 | 1167 | 1149 | 1132 | 1115 | 1097 | 1080 | 1063 | 3 | 6 | 9 | 12 | 14 |
| 84° | 1045 | 1028 | 1011 | 0993 | 0976 | 0958 | 0941 | 0924 | 0906 | 0889 | 3 | 6 | 9 | 12 | 14 |
| 85° | 0872 | 0854 | 0837 | 0819 | 0802 | 0785 | 0767 | 0750 | 0732 | 0715 | 3 | 6 | 9 | 12 | 14 |
| 86° | 0698 | 0680 | 0663 | 0645 | 0628 | 0610 | 0593 | 0576 | 0558 | 0541 | 3 | 6 | 9 | 12 | 15 |
| 87° | 0523 | 0506 | 0488 | 0471 | 0454 | 0436 | 0419 | 0401 | 0384 | 0366 | 3 | 6 | 9 | 12 | 15 |
| 88° | 0349 | 0332 | 0314 | 0297 | 0279 | 0262 | 0244 | 0227 | 0209 | 0192 | 3 | 6 | 9 | 12 | 15 |
| 89° | 0175 | 0157 | 0140 | 0122 | 0105 | 0087 | 0070 | 0052 | 0035 | 0017 | 3 | 6 | 9 | 12 | 15 |
N.B. - Numbers in difference column to be subtracted, not added.
| 0' | 6' | 12' | 18' | 24' | 30' | 36' | 42' | 48' | 54' | 1 | 2 | 3 | 4 | 5 | |
| 0° | .0000 | 0017 | 0035 | 0052 | 0070 | 0087 | 0105 | 0122 | 0140 | 0157 | 3 | 6 | 9 | 12 | 15 |
| 1 | .0175 | 0192 | 0209 | 0227 | 0244 | 0262 | 0279 | 0297 | 0314 | 0332 | 3 | 6 | 9 | 12 | 15 |
| 2 | .0349 | 0367 | 0384 | 0402 | 0419 | 0437 | 0454 | 0472 | 0489 | 0507 | 3 | 6 | 9 | 12 | 15 |
| 3 | .0524 | 0542 | 0559 | 0577 | 0594 | 0612 | 0629 | 0647 | 0664 | 0682 | 3 | 6 | 9 | 12 | 15 |
| 4 | .0699 | 0717 | 0734 | 0752 | 0769 | 0787 | 0805 | 0822 | 0840 | 0857 | 3 | 6 | 9 | 12 | 15 |
| 5 | .0875 | 0892 | 0910 | 0928 | 0945 | 0963 | 0981 | 0998 | 1016 | 1033 | 3 | 6 | 9 | 12 | 15 |
| 6 | .1051 | 1069 | 1086 | 1104 | 1122 | 1139 | 1157 | 1175 | 1192 | 1210 | 3 | 6 | 9 | 12 | 15 |
| 7 | .1228 | 1246 | 1263 | 1281 | 1299 | 1317 | 1334 | 1352 | 1370 | 1388 | 3 | 6 | 9 | 12 | 15 |
| 8 | .1405 | 1423 | 1441 | 1459 | 1477 | 1495 | 1512 | 1530 | 1548 | 1566 | 3 | 6 | 9 | 12 | 15 |
| 9 | .1584 | 1602 | 1620 | 1638 | 1655 | 1673 | 1691 | 1709 | 1727 | 1745 | 3 | 6 | 9 | 12 | 15 |
| 10 | .1763 | 1781 | 1799 | 1817 | 1835 | 1853 | 1871 | 1890 | 1908 | 1926 | 3 | 6 | 9 | 12 | 15 |
| 11 | .1944 | 1962 | 1980 | 1998 | 2016 | 2035 | 2053 | 2071 | 2089 | 2107 | 3 | 6 | 9 | 12 | 15 |
| 12 | .2126 | 2144 | 2162 | 2180 | 2199 | 2217 | 2235 | 2254 | 2272 | 2290 | 3 | 6 | 9 | 12 | 15 |
| 13 | .2309 | 2327 | 2345 | 2364 | 2382 | 2401 | 2419 | 2438 | 2456 | 2475 | 3 | 6 | 9 | 12 | 15 |
| 14 | .2493 | 2512 | 2530 | 2549 | 2568 | 2586 | 2605 | 2623 | 2642 | 2661 | 3 | 6 | 9 | 12 | 16 |
| 15 | .2679 | 2698 | 2717 | 2736 | 2754 | 2773 | 2792 | 2811 | 2830 | 2849 | 3 | 6 | 9 | 13 | 16 |
| 16 | .2867 | 2886 | 2905 | 2924 | 2943 | 2962 | 2981 | 3000 | 3019 | 3038 | 3 | 6 | 9 | 13 | 16 |
| 17 | .3057 | 3076 | 3096 | 3115 | 3134 | 3153 | 3172 | 3191 | 3211 | 3230 | 3 | 6 | 10 | 13 | 16 |
| 18 | .3249 | 3269 | 3288 | 3307 | 3327 | 3346 | 3365 | 3385 | 3404 | 3424 | 3 | 6 | 10 | 13 | 16 |
| 19 | .3443 | 3463 | 3482 | 3502 | 3522 | 3541 | 3561 | 3581 | 3600 | 3620 | 3 | 7 | 10 | 13 | 16 |
| 20 | .3640 | 3659 | 3679 | 3699 | 3719 | 3739 | 3759 | 3779 | 3799 | 3819 | 3 | 7 | 10 | 13 | 17 |
| 21 | .3839 | 3859 | 3879 | 3899 | 3919 | 3939 | 3959 | 3979 | 4000 | 4020 | 3 | 7 | 10 | 13 | 17 |
| 22 | .4040 | 4061 | 4081 | 4101 | 4122 | 4142 | 4163 | 4183 | 4204 | 4224 | 3 | 7 | 10 | 14 | 17 |
| 23 | .4245 | 4265 | 4286 | 4307 | 4327 | 4348 | 4369 | 4390 | 4411 | 4431 | 3 | 7 | 10 | 14 | 17 |
| 24 | .4452 | 4473 | 4494 | 4515 | 4536 | 4557 | 4578 | 4599 | 4621 | 4642 | 3 | 7 | 10 | 14 | 18 |
| 25 | .4663 | 4684 | 4706 | 4727 | 4748 | 4770 | 4791 | 4813 | 4834 | 4856 | 4 | 7 | 11 | 14 | 18 |
| 26 | .4877 | 4899 | 4921 | 4942 | 4964 | 4986 | 5008 | 5029 | 5051 | 5073 | 4 | 7 | 11 | 14 | 18 |
| 27 | .5095 | 5117 | 5139 | 5161 | 5184 | 5206 | 5228 | 5250 | 5272 | 5295 | 4 | 7 | 11 | 15 | 18 |
| 28 | .5317 | 5340 | 5362 | 5384 | 5407 | 5430 | 5452 | 5475 | 5498 | 5520 | 4 | 7 | 11 | 15 | 19 |
| 29 | .5543 | 5566 | 5589 | 5612 | 5635 | 5658 | 5681 | 5704 | 5727 | 5750 | 4 | 8 | 11 | 15 | 19 |
| 30 | .5774 | 5797 | 5820 | 5844 | 5867 | 5890 | 5914 | 5938 | 5961 | 5985 | 4 | 8 | 12 | 16 | 20 |
| 31 | .6009 | 6032 | 6056 | 6080 | 6104 | 6128 | 6152 | 6176 | 6200 | 6224 | 4 | 8 | 12 | 16 | 20 |
| 32 | .6249 | 6273 | 6297 | 6322 | 6346 | 6371 | 6395 | 6420 | 6445 | 6469 | 4 | 8 | 12 | 16 | 20 |
| 33 | .6494 | 6519 | 6544 | 6569 | 6594 | 6619 | 6644 | 6669 | 6694 | 6720 | 4 | 8 | 12 | 17 | 21 |
| 34 | .6745 | 6771 | 6796 | 6822 | 6847 | 6873 | 6899 | 6924 | 6950 | 6976 | 4 | 8 | 13 | 17 | 21 |
| 35 | .7002 | 7028 | 7054 | 7080 | 7107 | 7133 | 7159 | 7186 | 7212 | 7239 | 4 | 9 | 13 | 17 | 22 |
| 36 | .7265 | 7292 | 7319 | 7346 | 7373 | 7400 | 7427 | 7454 | 7481 | 7508 | 4 | 9 | 13 | 18 | 22 |
| 37 | .7536 | 7563 | 7590 | 7618 | 7646 | 7673 | 7701 | 7729 | 7757 | 7785 | 5 | 9 | 14 | 18 | 23 |
| 38 | .7813 | 7841 | 7869 | 7898 | 7926 | 7954 | 7983 | 8012 | 8040 | 8069 | 5 | 9 | 14 | 19 | 24 |
| 39 | .8098 | 8127 | 8156 | 8185 | 8214 | 8243 | 8273 | 8302 | 8332 | 8361 | 5 | 10 | 15 | 19 | 24 |
| 40 | .8391 | 8421 | 8451 | 8481 | 8511 | 8541 | 8571 | 8601 | 8632 | 8662 | 5 | 10 | 15 | 20 | 25 |
| 41 | .8693 | 8724 | 8754 | 8785 | 8816 | 8847 | 8878 | 8910 | 8941 | 8972 | 5 | 10 | 15 | 21 | 26 |
| 42 | .9004 | 9036 | 9067 | 9099 | 9131 | 9163 | 9195 | 9228 | 9260 | 9293 | 5 | 11 | 16 | 21 | 27 |
| 43 | .9325 | 9358 | 9391 | 9424 | 9457 | 9490 | 9523 | 9556 | 9590 | 9623 | 5 | 11 | 16 | 22 | 28 |
| 44 | .9657 | 9691 | 9725 | 9759 | 9793 | 9827 | 9861 | 9896 | 9930 | 9965 | 6 | 11 | 17 | 23 | 29 |
| 0' | 6' | 12' | 18' | 24' | 30' | 36' | 42' | 48' | 54' | 1 | 2 | 3 | 4 | 5 | |
| 45° | .00000 | 0035 | 0070 | 0105 | 0141 | 0176 | 0212 | 0247 | 0283 | 0319 | 6 | 12 | 18 | 24 | 30 |
| 46 | 1.0355 | 0392 | 0428 | 0464 | 0501 | 0538 | 0575 | 0612 | 0649 | 0686 | 6 | 12 | 18 | 24 | 31 |
| 47 | 1.0724 | 0761 | 0799 | 0837 | 0875 | 0913 | 0951 | 0990 | 1028 | 1067 | 6 | 13 | 19 | 25 | 32 |
| 48 | 1.1106 | 1145 | 1184 | 1224 | 1263 | 1303 | 1343 | 1383 | 1423 | 1463 | 7 | 13 | 20 | 26 | 33 |
| 49 | 1.1504 | 1544 | 1585 | 1626 | 1667 | 1708 | 1750 | 1792 | 1833 | 1875 | 7 | 14 | 20 | 27 | 34 |
| 50 | 1.1918 | 1960 | 2002 | 2045 | 2088 | 2131 | 2174 | 2218 | 2261 | 2305 | 7 | 14 | 21 | 29 | 36 |
| 51 | 1.2349 | 2393 | 2437 | 2482 | 2527 | 2572 | 2617 | 2662 | 2708 | 2753 | 7 | 15 | 22 | 30 | 37 |
| 52 | 1.2799 | 2846 | 2892 | 2938 | 2985 | 3032 | 3079 | 3127 | 3175 | 3222 | 8 | 15 | 23 | 31 | 39 |
| 53 | 1.3270 | 3319 | 3367 | 3416 | 3465 | 3514 | 3564 | 3613 | 3663 | 3713 | 8 | 16 | 24 | 33 | 41 |
| 54 | 1.3764 | 3814 | 3865 | 3916 | 3968 | 4019 | 4071 | 4124 | 4176 | 4229 | 8 | 17 | 26 | 34 | 43 |
| 55 | 1.4281 | 4335 | 4388 | 4442 | 4496 | 4550 | 4605 | 4659 | 4715 | 4770 | 9 | 18 | 27 | 36 | 45 |
| 56 | 1.4826 | 4882 | 4938 | 4994 | 5051 | 5108 | 5166 | 5224 | 5282 | 5340 | 9 | 19 | 28 | 38 | 48 |
| 57 | 1.5399 | 5458 | 5517 | 5577 | 5637 | 5697 | 5757 | 5818 | 5880 | 5941 | 10 | 20 | 30 | 40 | 50 |
| 58 | 1.6003 | 6066 | 6128 | 6191 | 6255 | 6319 | 6383 | 6447 | 6512 | 6577 | 10 | 21 | 32 | 42 | 53 |
| 59 | 1.6643 | 6709 | 6775 | 6842 | 6909 | 6977 | 7045 | 7113 | 7182 | 7251 | 11 | 22 | 33 | 45 | 56 |
| 60 | 1.7321 | 7391 | 7461 | 7532 | 7603 | 7675 | 7747 | 7820 | 7893 | 7966 | 12 | 23 | 35 | 48 | 60 |
| 61 | 1.8040 | 8115 | 8190 | 8265 | 8341 | 8418 | 8495 | 8572 | 8650 | 8728 | 12 | 25 | 38 | 51 | 64 |
| 62 | 1.8807 | 8887 | 8967 | 9047 | 9128 | 9210 | 9292 | 9375 | 9458 | 9542 | 13 | 27 | 40 | 54 | 68 |
| 63 | 1.9626 | 9711 | 9797 | 9883 | 9970 | 0̅057 | 0̅145 | 0̅233 | 0̅323 | 0̅413 | 14 | 29 | 43 | 58 | 73 |
| 64 | 2.0503 | 0594 | 0686 | 0778 | 0872 | 0965 | 1060 | 1155 | 1251 | 1348 | 15 | 31 | 46 | 62 | 78 |
| 65 | 2.1445 | 1543 | 1642 | 1742 | 1842 | 1943 | 2045 | 2148 | 2251 | 2355 | 16 | 33 | 50 | 67 | 84 |
| 66 | 2.2460 | 2566 | 2673 | 2781 | 2889 | 2998 | 3109 | 3220 | 3332 | 3445 | 18 | 36 | 54 | 72 | 91 |
| 67 | 2.3559 | 3673 | 3789 | 3906 | 4023 | 4142 | 4262 | 4383 | 4504 | 4627 | 19 | 39 | 58 | 78 | 99 |
| 68 | 2.4751 | 4876 | 5002 | 5129 | 5257 | 5386 | 5517 | 5649 | 5782 | 5916 | 21 | 42 | 64 | 85 | 108 |
| 69 | 2.6051 | 6187 | 6325 | 6464 | 6605 | 6746 | 6889 | 7034 | 7179 | 7326 | 23 | 46 | 70 | 94 | 118 |
| 70 | 2.7475 | 7625 | 7776 | 7929 | 8083 | 8239 | 8397 | 8556 | 8716 | 8878 | 25 | 50 | 76 | 103 | 130 |
| 71 | 2.9042 | 9208 | 9375 | 9544 | 9714 | 9887 | 0̅061 | 0̅237 | 0̅415 | 0̅595 | 28 | 56 | 84 | 114 | 144 |
| 72 | 3.0777 | 0961 | 1146 | 1334 | 1524 | 1716 | 1910 | 2106 | 2305 | 2506 | 31 | 62 | 94 | 127 | 160 |
| 73 | 3.2709 | 2914 | 3122 | 3332 | 3544 | 3759 | 3977 | 4197 | 4420 | 4646 | 34 | 69 | 105 | 142 | 179 |
| 74 | 3.4874 | 5105 | 5339 | 5576 | 5816 | 6059 | 6305 | 6554 | 6806 | 7062 | 39 | 78 | 118 | 160 | 202 |
| 75 | 3.7321 | 7583 | 7848 | 8118 | 8391 | 8667 | 8947 | 9232 | 9520 | 9812 | 44 | 89 | 135 | 182 | 230 |
| 76 | 4.0108 | 0408 | 0713 | 1022 | 1335 | 1653 | 1976 | 2303 | 2635 | 2972 | 50 | 102 | 154 | 209 | 265 |
| 77 | 4.3315 | 3662 | 4015 | 4373 | 4737 | 5107 | 5483 | 5864 | 6252 | 6646 | 58 | 118 | 179 | 243 | 308 |
| 78 | 4.7046 | 7453 | 7867 | 8288 | 8716 | 9152 | 9594 | 0̅045 | 0̅504 | 0̅970 | 68 | 138 | 210 | 285 | 363 |
| 79 | 5.1446 | 1929 | 2422 | 2924 | 3435 | 3955 | 4486 | 5026 | 5578 | 6140 | 81 | 164 | 251 | 341 | 434 |
| 80 | 5.6713 | 7297 | 7894 | 8502 | 9124 | 9758 | 0̅405 | 1̅066 | 1̅742 | 2̅432 | * | ||||
| 81 | 6.3138 | 3859 | 4596 | 5350 | 6122 | 6912 | 7720 | 8548 | 9395 | 0̅264 | |||||
| 82 | 7.1154 | 2066 | 3002 | 3962 | 4947 | 5958 | 6996 | 8062 | 9158 | 0̅285 | |||||
| 83 | 8.1443 | 2636 | 3863 | 5126 | 6427 | 7769 | 9152 | 0̅579 | 2̅052 | 3̅572 | |||||
| 84 | 9.5144 | 9.677 | 9.845 | 10.02 | 10.20 | 10.39 | 10.58 | 10.78 | 10.99 | 11.20 | |||||
| 85 | 11.43 | 11.66 | 11.91 | 12.16 | 12.43 | 12.71 | 13.00 | 13.30 | 13.62 | 13.95 | |||||
| 86 | 14.30 | 14.67 | 15.06 | 15.46 | 15.89 | 16.35 | 16.83 | 17.34 | 17.89 | 18.46 | |||||
| 87 | 19.08 | 19.74 | 20.45 | 21.20 | 22.02 | 22.90 | 23.86 | 24.90 | 26.03 | 27.27 | |||||
| 88 | 28.64 | 30.14 | 31.82 | 33.69 | 35.80 | 38.19 | 40.92 | 44.07 | 47.74 | 52.08 | |||||
| 89 | 57.29 | 63.66 | 71.62 | 81.85 | 95.49 | 114.6 | 143.2 | 191.0 | 286.5 | 573.0 | |||||
[*] Difference columns cease to be useful, owing to the¶ rapidity with which the value of the tangent changes.
[**TRANSCRIBER'S NOTE: In the second Natural Tangents table, overlines
are applied to values that exceed ten times the previous values in the
row. The first example is in cell for 63° 36', where the first 0 has an
overline. If the overlines are not present, please access the HTML
version of this eBook.]
144
145
[BLANK PAGE]
ANSWERS TO PROBLEMS
[BLANK PAGE]
ANSWERS TO PROBLEMS
CHAPTER I
1. \(2a + 6b + 6c − 3d\).
2. \(−9a + b − 6c\).
3. \(3d − z + 14b − 10a\).
4. \(−3x + 6y + 4z + a\).
5. \(−8b + 9a − 2c\).
6. \(−8x − 6a + 4b + 11y\).
7. \(2x − 2y + 28z\).
CHAPTER II
1. \(18a^2b^2\).
2. \(48a^2b^2c^3\).
3. \(90x^2y^2\).
4 \(144a^8b^5c^2\).
5. \(abc^2\).
6. \(\frac{a^2b^3c^2}{d}\).
7. \(a^4b^5c\).
8. \(a^8b^2c^7\).
9. \(\frac{a^2c^2z}{b^4}\).
10. \(\frac{40a^7}{c^4}\).
11. \(\frac{b^2c^2}{54ad}\).
CHAPTER III
1. \(\frac{9a^2b^3c}{4x}\).
2. \(\frac{bc}{18d}\).
3. \(\frac{a^4b^4c^2x}{6y^2}\).
4. \(20x^2 + 15xy + 10xz\).
5. \(4a + 2a^2b^2 − b\).
6. \(a^2 − b^2\).
7. \(6a^2 − ab + 5ac − 2b^2 + 6bc − 4c^2\).
8. \(a − b\).
9. \(a^2 + 2ab + b^2\).
10. \(\frac{a + b}{a − b}\).
11. \(\frac{3a^2c − 2a^2d + 3ac^2 − 3acd}{2ac + 2ad − 2c^2 − 2cd}\).
12. \(\frac{c^3ba}{12}\).
13. \(\frac{8a + b^2 + 4c}{4b}\).
14. \(\frac{4 − 12a + a^2c}{6a^2}\).
15. \(\frac{120a^2c + 3bc − 6bx + 2bcd}{12bc}\).
16. \(\frac{3ab − ac + 2b^2}{4ab}\).
17. \(\frac{5a^2 − 2a − 2b}{5a^2 + 5ab}\).
148
CHAPTER IV
1. \(3, 2, 5, a, a, b\).
2. \(3, 2, 2, 2, 2, a, a, a, a, c\).
3. \(3, 2, 5, x, x, y, y, y, y, z, z, z\).
4. \(3, 3, 2, 2, 2, 2, x, x, a, a\).
5. \(3, 2, 2, \frac{1}{2}, \frac{1}{2}, a, \frac{1}{a}, \frac{1}{a}, b, b, \frac{1}{b}, \frac{1}{b}, c, c, c\).
6. \(2, 5, \frac{1}{2}, x, \frac{1}{x}, \frac{1}{x}, y, y, \frac{1}{y}\).
7. \((a − c)(2a + b)\).
8. \((3x + y)(x + c)\).
9. \((2x + 5y)(x + z)\).
10. \((a − b)(a − b)\).
11. \((2x − 3y)(2x − 3y)\).
12. \((9a + 5b)(9a + 5b)\).
13. \((4c − 6a)(4c − 6a)\).
14. \(x, y, (4x^2 + 5zy − 10z)\).
15. \(5b(6a + 3ac − c)\).
16. \((9xy − 5a) (9xy + 5a)\).
17. \((a^2 + 4b^2)(a + 2b)(a − 2b)\).
18. \((12x^2y + 8z)(12x^2y − 8z)\).
19. \((a^2 − 2ac + c) 2\), \(2\).
20. \((4y + x)(4y + x)\).
21. \((3y + 2x)(2y − 3x)\).
22. \((40 + 56) (a − 26)\).
23. \((3y − 2x)(2y − 3x)\).
24. \((2a + b)(a − 3b)\).
25. \((2a + 5b)(a + 2b)\).
CHAPTER V
Square roots.
1. \(4x + 3y\).
2. \(2a + 6b\).
3. \(6x + 2y\).
4. \(5a − 2b\).
5. \(a + b + c\).
Cube roots.
1. \(2x + 3y\).
2. \(x + 2y\).
3. \(3a + 3b\).
149
CHAPTER VI
1. \(x = 4\frac{2}{3}\).
2. \(x = 2\frac{1}{3}\).
3. \(x = 4\).
4. \(x = −\frac{5}{19}\).
5. \(x = \frac{5}{28}\).
6. \(x = 30\).
7. \(x = 6\frac{133}{168}\).
8. \(x = \frac{9a + 9b − ay − by}{3}\).
9. \(x = −\frac{3(a − b) + 2a^2}{2a(a − b)(a + 1)}\).
10. \(x = \frac{10(a^2 − b^2)}{2a}\).
11. \(2a^2x + 2ab − ax^2 − bx = c^2x − bc + 10cx − 10b\).
12. \(\frac{ax}{3} + bx = \frac{cy}{d} + \frac{3c}{d}\).
13. \(a −b = \frac{c}{c + 3}\).
14. \(2 = \frac{10y}{y + 2}\).
15. \(5a + 3 = x + d + 3\).
16. \(6ax − 5y = 5 − 10x\).
17. \(15z^2 + 4x = 12 − 10y\).
18. \(6a + 2d = 4\).
19. \(3x − 2 = 3x^2 − y\).
20. \(8x − 10cy = 20y\).
21. \(\frac{x^2}{(c − d)(3a + b)} − \frac{x^2}{3(c − d)} = 2a + b\).
22. \(x = −\frac{1}{2}\).
23. Coat costs \$28.57.
Gun costs \$57.14.
Hat costs \$14.29.
Gun costs \$57.14.
Hat costs \$14.29.
24. Horse costs \$671.66.
Carriage costs \$328.33.
Carriage costs \$328.33.
25. Anne’s age is 18 years.
26. 24 chairs and 14 tables.
CHAPTER VII
1. \(y = 4, x = 2\).
2. \(1 = 5, y = 2\).
3. \(x = 1, y = 2\).
4. \(x = 5, y = 2, z = 3\).
5. \(x = 3, y = 2, z = 4\).
6. \(x = −15, y = 15\).
7. \(x = −.084, y = -10.034\).
8. \(x = 5\frac{1}{22}, y = -\frac{3}{22}\).
9. \(x = −1.1, y = 6.1\).
10. \(x = 1\frac{3}{22}, y = 2\frac{5}{22}\).
150
CHAPTER VIII
1. \(x = 2\) or \(x = 1\).
2. \(x = \frac{−2 ± 2\sqrt{19}}{3}\).
3. \(x = 2\).
4. \(x = 4\) or \(−2\).
5. \(x = 3\) or \(1\).
6. \(x = ± 2\) or \(± \sqrt{−6} \).
7. \(x = −\frac{5 ± \sqrt{305}}{14a}\).
8. \(x = −\frac{a ± \sqrt{12ab^2 + a^2}}{2b}\).
9. \(x = −\frac{1 − 3a ± \sqrt{51a^2 − 6a + 1}}{2a}\).
10. \(x = +\frac{3(a + b) ± \sqrt{8 (a + b) + 9(a + b)^2}}{2}\).
11. \(x = −\frac{5 ± \sqrt{205}}{6}\).
12. \(x = −3\).
13. \(x = 4(2 ± \sqrt{3})\).
14. \(x = −\frac{3}{4a}\).
15. \(x = \frac{2ab}{a + b}\).
16. \(x = −\frac{27 ± \sqrt{2425}}{16}\).
17. \(x = −\frac{3 ± \sqrt{−7}}{2}\).
18. \(x = −\frac{1±\sqrt{−299}}{6}\).
19. \(x = 63\).
20. \(x = 100a^2 − 301a + 225\).
21. \(x = \frac{a^2 ± a\sqrt{a^2 + 4}}{2}\).
22. \(x = \frac{−5 ± \sqrt{5}}{6}\).
CHAPTER IX
1. \(k = 50\).
2. \(b = \sqrt{\frac{1}{441}}\).
3. \(k = 60\).
4. \(a = 192\).
5. \(c = 5\).
CHAPTER X
1. 96 sq. ft.
2. 180 sq. ft.
3. 254.469 sq. ft.
4. Hypotenuse = \(\sqrt{117}\) ft. long.
5. 62.832 ft. long.
6. \(\sqrt{301}\) ft. long.
7. 27.6 ft. long.
8. 7957.7 miles.
9. Altitude = 7.5 ft.
10. Altitude = 4 ft.
151
CHAPTER XI
1. sine = .5349; cosine = .8456; tangent = .6330.
2. sine = .9888; cosine = .1495; tangent = 6.6122.
3. \(25° 36'\).
4. \(79° 25'\).
5. \(36° 59'\).
6. \(28° 54'\).
7. \(c = 600\) ft.; \(b = 519.57\) ft.
8. \(\measuredangle a = 57° 47'; c = 591.01\) ft.
9. \(a = 1231\) ft.; \(b = 217\) ft.
10. \(\measuredangle a = 61° 51'; a = 467.3\) ft.
CHAPTER XII
1. 3.5879.
2. 1.8667.
3. −3.9948.
4. 4.6155.
5. 666.2.
6. 74430.
7. .2745.
8. .00024105.
9. 2302.5.
10. 9,802,000.
11. 24,860,000.
12. 778,500,000.
13. .000286.
14. .0001199.
15. 32.34.
16. 111.6.
17. .0323.
18. .03767.
19. 1,198,000.
20. 18,410,000.
21. 275,500.
22. .00001314.
23. 549.7.
24. 4.27.
25. .296.
26. 46.86.
CHAPTER XIII
Get cross-section paper and plot the following corresponding
values of x and y and the result will be the line or curve
as the case may be.
152
3. \(x = 0; y = −2\) .
\(y = 0; x = 4\) . }
A straight line.
4. \(x = 0; y = −\tfrac{8}{10}\) .
\(y = 0; x = −2\tfrac{2}{3}\) . }
A straight line.
5. \(x = 0; y = ±6\) .
\(y = 0; x = ±6\) .
\(x = 1; y = ±\sqrt{35}\) .
\(x = 2; y = ±\sqrt{32}\) .
\(x = 3; y = ±\sqrt{27}\) .
\(x = 4; y = ±\sqrt{20}\) .
\(x = 5; y = ±\sqrt{11}\) .
}
This is a circle with its center at the¶
intersection of the x and y axes and¶
with a radius of 6.
6. \(y = 0; x = 0\) .
\(y = 2; x = ±\sqrt{32}\) .
\(y = 4; x = ±8\) .
\(y = 6; x = ±\sqrt{96}\) . }
This is a parabola and to plot it¶
correctly a great many corresponding¶
values of x and y are necessary.
7. \(y = 0; x = ±4\) .
\(y = ±1; x = ±\sqrt{17}\) .
\(y = ±3; x = ±5\) .
\(y = 5; x = +\sqrt{41}\) .
}
This is an hyperbola and a great many¶
corresponding values of x and y are¶
necessary in order to plot the curve¶
correctly.
8. \(y = 0; x = ±\sqrt{7}\) .
\(x = 0; y = +7\) or \(−3\) .
\(x = 1; y = 2 ±\sqrt{22}\) .
\(x = 2; y = 2 ±\sqrt{13}\) .
}
This is an ellipse with its center¶
at +2 on the y axis. A great many¶
corresponding values of x and y are¶
necessary to plot it correctly.
fin
Appendix A
fig
Appendix B
|
1. \(x = 0; y = −3\tfrac{1}{3}\) . \(y = 0; x = 10\) . \(x = 22; y = 4\) . \(x = −2; y = −4\) . | } | This is a straight line and only two¶ pairs of corresponding values of x and¶ y are necessary to draw it. |
|
2. \(x = 0; y = 3\) . \(y = 0; x = 7\tfrac{1}{2}\) . | } | This is also a straight line. |
\(y = 0; x = 4\) .
\(y = 0; x = −2\tfrac{2}{3}\) .
\(y = 0; x = ±6\) .
\(x = 1; y = ±\sqrt{35}\) .
\(x = 2; y = ±\sqrt{32}\) .
\(x = 3; y = ±\sqrt{27}\) .
\(x = 4; y = ±\sqrt{20}\) .
\(x = 5; y = ±\sqrt{11}\) .
\(y = 2; x = ±\sqrt{32}\) .
\(y = 4; x = ±8\) .
\(y = 6; x = ±\sqrt{96}\) .
\(y = ±1; x = ±\sqrt{17}\) .
\(y = ±3; x = ±5\) .
\(y = 5; x = +\sqrt{41}\) .
\(x = 0; y = +7\) or \(−3\) .
\(x = 1; y = 2 ±\sqrt{22}\) .
\(x = 2; y = 2 ±\sqrt{13}\) .
Intersections of Curves
|
1. \(x = 2\tfrac{2}{7};\) \(y = 3\tfrac{1}{7}\) . | } | This is the intersection of 2¶ straight lines. |
|
2. \(y = −5 ± \sqrt{\tfrac{31}{2}}\) ; \(x = 5 ± \sqrt{\tfrac{31}{2}}\) . | } | This is the intersection of a¶ straight line and a circle. |
3. The roots are here imaginary showing that the two
curves do not touch at all, which can be easily shown by
plotting them.
CHAPTER XIV
1. \(6x^2 \,\delta x\).
2. \(24 × \,\delta x\).
3. \(40 × \,\delta x\).
4. \(6x \,\delta x + 4 \,\delta x = 15 x^2 \,\delta x\).
5. \(8y \,\delta y − 3x_{y} \,\delta y\).
6. \(42 y^4x^2 \,\delta x + 56 x^3y^3 \,\delta y\).
7. \(\frac{2 yx \,\delta x − x^2 \,\delta y}{y^2}\).
8. \(4y \,\delta y − 4qx_{y} \,\delta y\).
9. \(y_{x} = −\frac{x}{2y}\).
10. \(y_{x} = −3x^2\).
11. \(y_{x} = \frac{x}{y}\).
12. \(y_{x} = −\frac{y}{x}\).
13. \(41° 48' 10''\).
14. When \(x = 0\) at which time \(y\) also \(= 0\).
15. \(\frac{x^4}{2}\).
16. \(\frac{5x^3}{3}\).
17. \(5 ax^2 + \frac{5}{3} x^3 + 3x\).
18. \(−3\ cos\ x\).
19. \(2\ sine\ x\).
20. \(117\).
21. \(8.7795\).
22. \(10\ cosine\ x \,\delta x\).
23. \(cos^2\ x dx −\ sin^2\ x dx\).
24. \(\frac{1}{x} dx\).
25. \(\frac{2x^2y \,\delta y − 2y^2x \,\delta x}{x^4}\).
Appendix A
Transcriber’s Notes
TRANSCRIBER'S NOTES
- New original cover art included with this eBook is granted to the public domain.¶
- A few minor spelling errors and edits were made. (Page 8: “Indentity of Symbols.”; Page 85: “…the Naperian or…”; Page 117: “…the dffierential of…”)¶
- Images and page breaks that originally broke paragraphs have been moved before or after the paragraph breaks as needed. The page numbers from the table of contents are still correctly associated.¶
- The footnotes on pages 92, 131 and 143 have been placed directly following the elements that are referenced.¶
- On pages 23, 28 and 46 a header for 'PROBLEMS' has been restored, corresponding with the other 13 chapters in the book. This will facilitate finding the these important sections.¶
- Figures have been redrawn in order to improve the readability on both high-density screens and smaller physical sizes.¶
- The overstroke numerals in the logarithm tables may not be visible in some reader clients and formats.¶
- The typeface used in the logarithm and trigonometry tables has been set in a narrow typeface for readability.¶
- Plain Text Note: the uppercase version of the Greek letter DELTA ('\(\Delta \) ') is used in place of the lowercase DELTA ('\(\delta \) '), used to denote differential, in order to improve legibility.¶
- Plain Text Note: tables for logarithms and trigonometry are very difficult to use, due to the limits of a 72 character screen width. In order to properly use these tables, please view any of the other versions of this eBook. If you must use the plain text version, they have been split into groups of columns in order to fit the text width.¶
- Plain Text Note: Fractions are shown as ( _numerator_ )⁄( _denominator_ ), and square roots are shown as √{radican}, and roots with other indexes are shown as \sqrt{index}{radican}. (See page 91 for sole example.)
Appendix B
Figures
Fig. 1
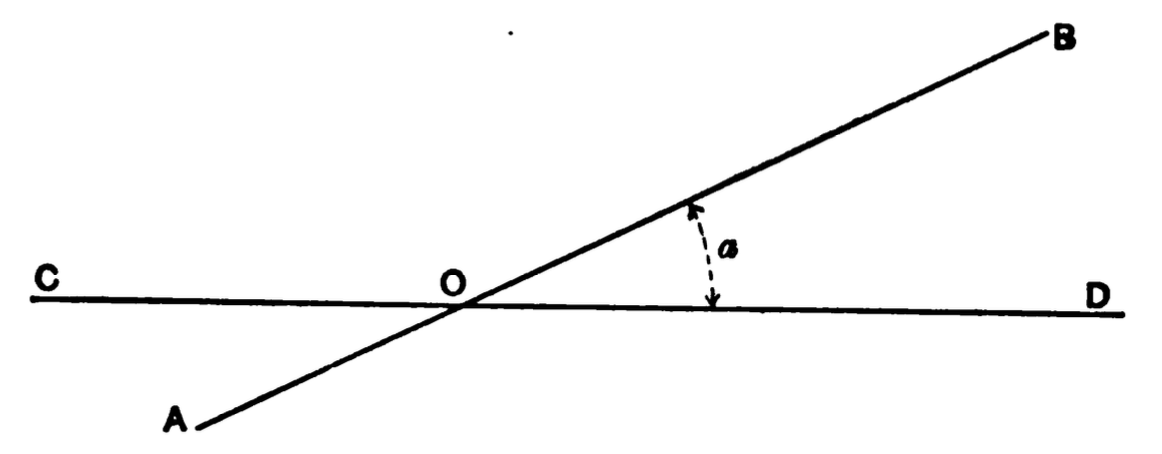


Fig. 2



Fig. 3


Fig. 4


Fig. 5


Fig. 6



Fig. 7
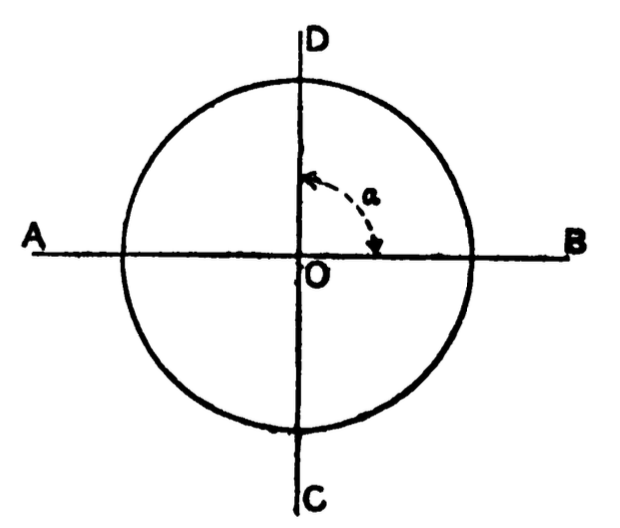


Fig. 8


Fig. 9


Fig. 10



Fig. 11
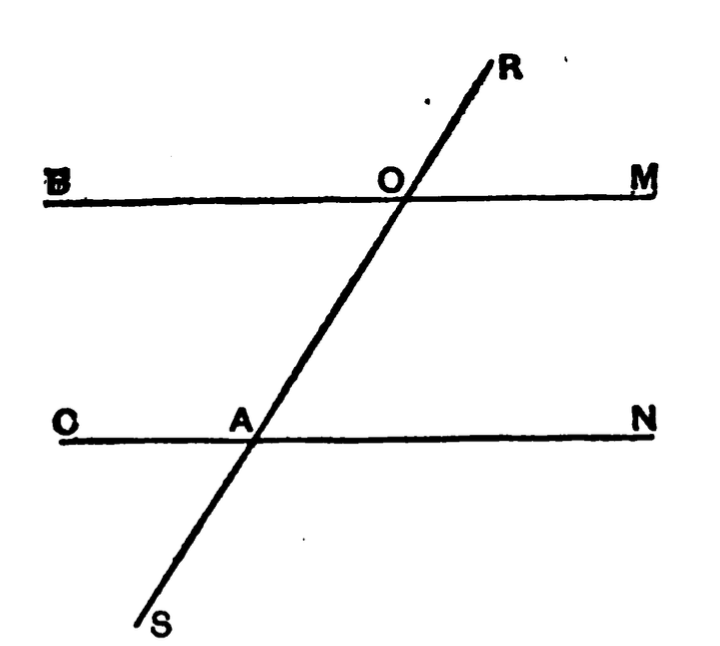


Fig. 12
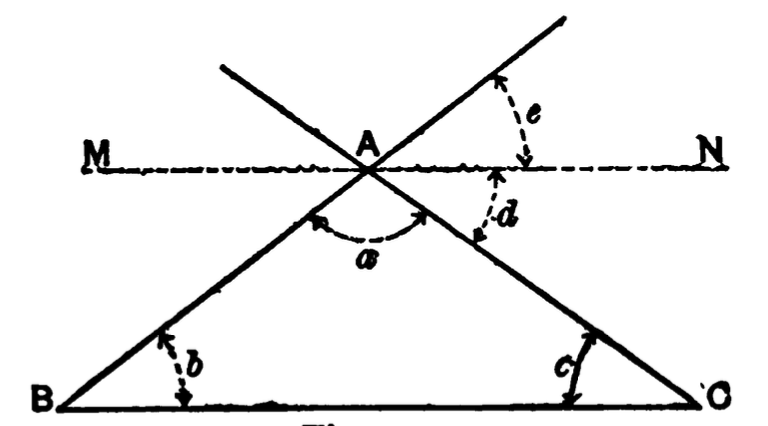


Fig. 13


Fig. 14


Fig. 15
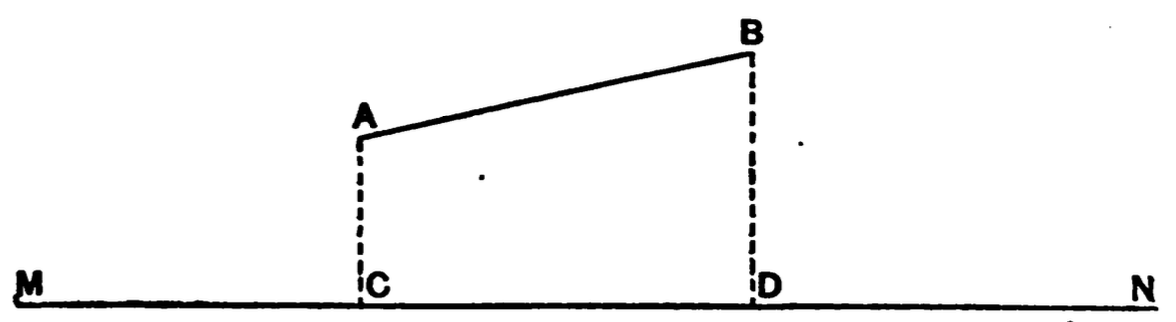


Fig. 16
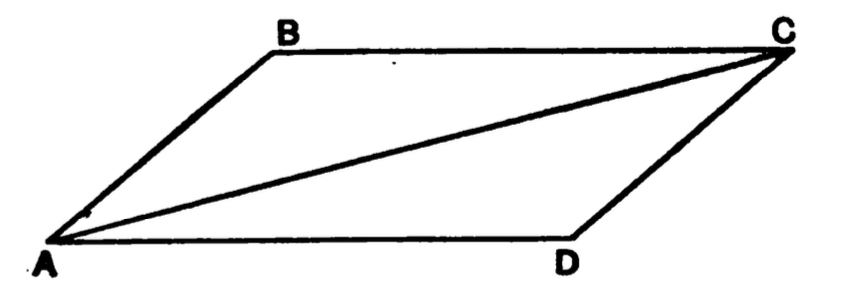


Fig. 17
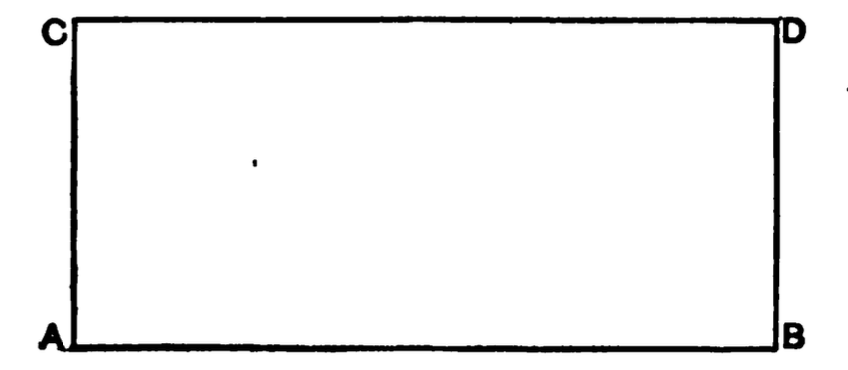


Fig. 18
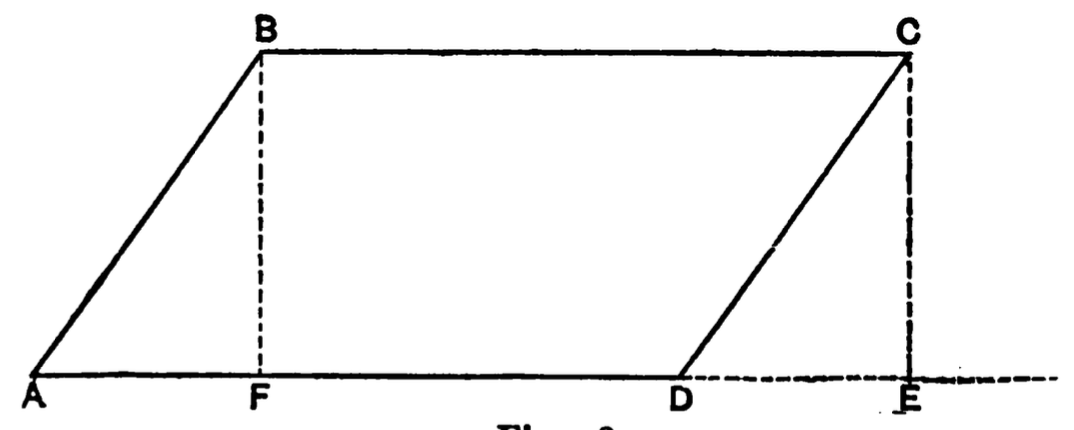


Fig. 19
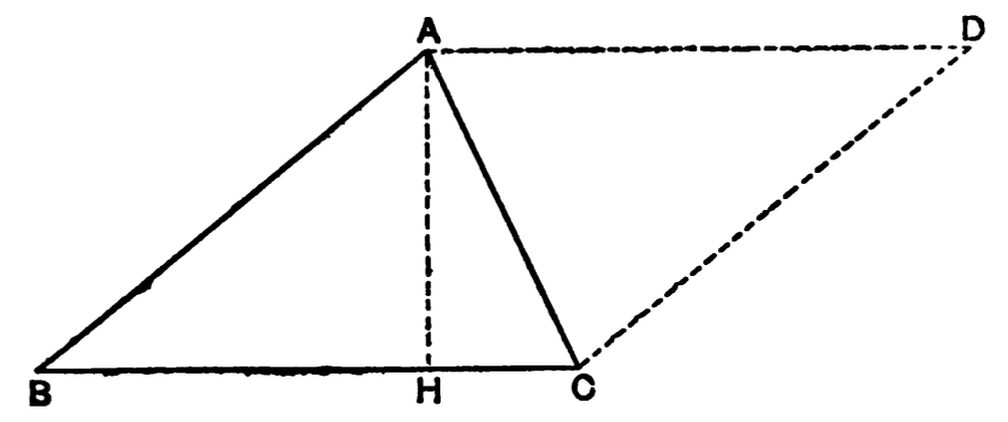


Fig. 20
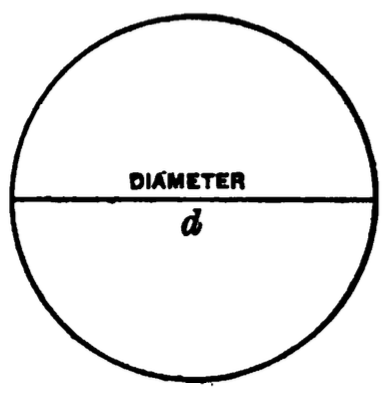


Fig. 21
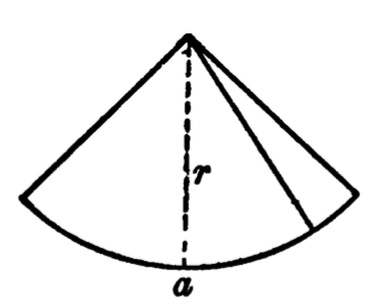


Fig. 22


Fig. 23
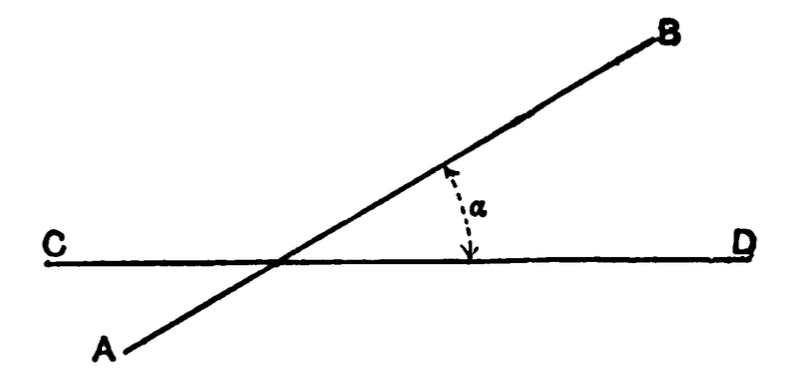


Fig. 24
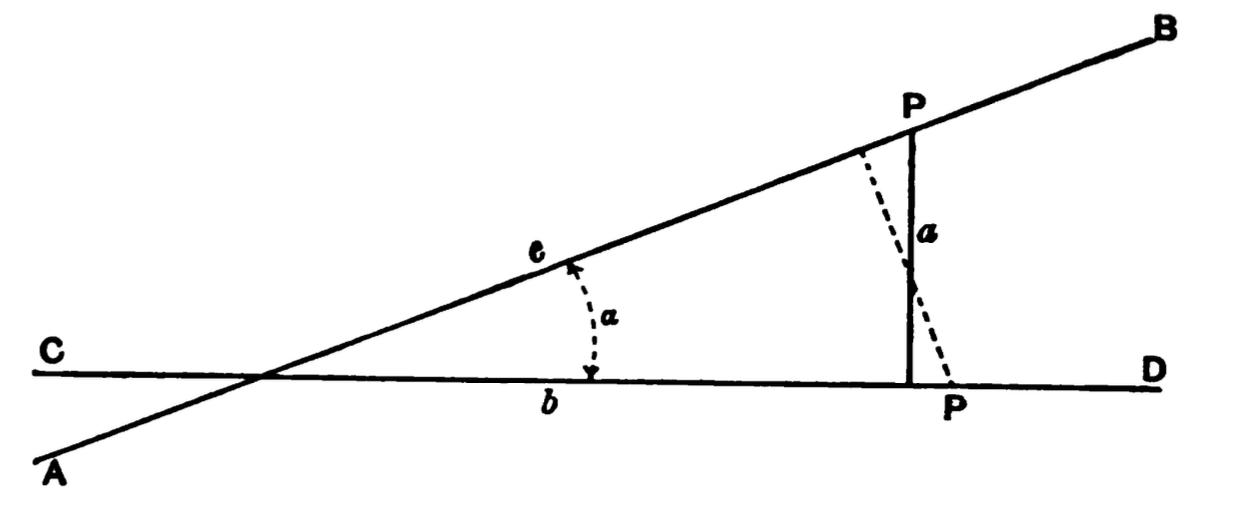


Fig. 25
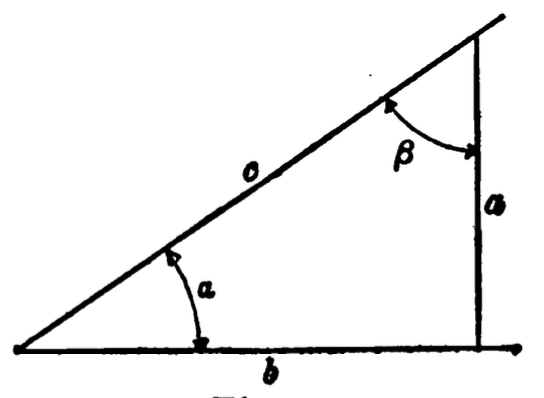


Fig. 26
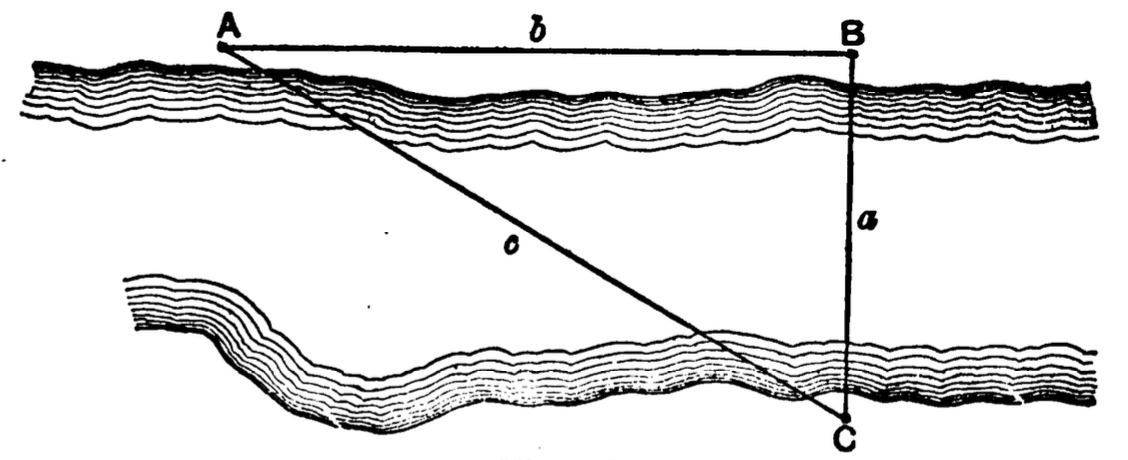


Fig. 27
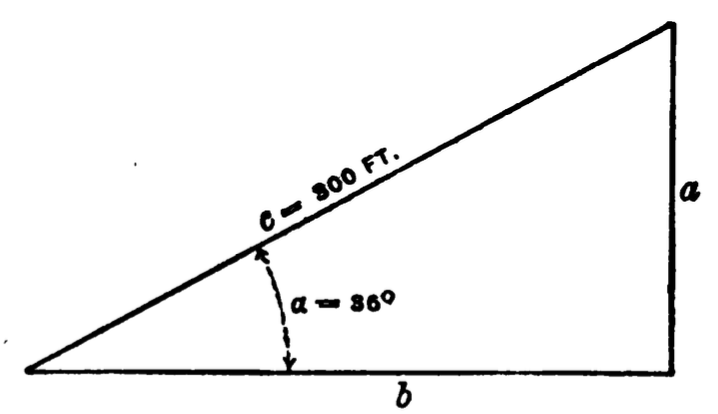


Fig. 28


Fig. 29


Fig. 30


Fig. 31
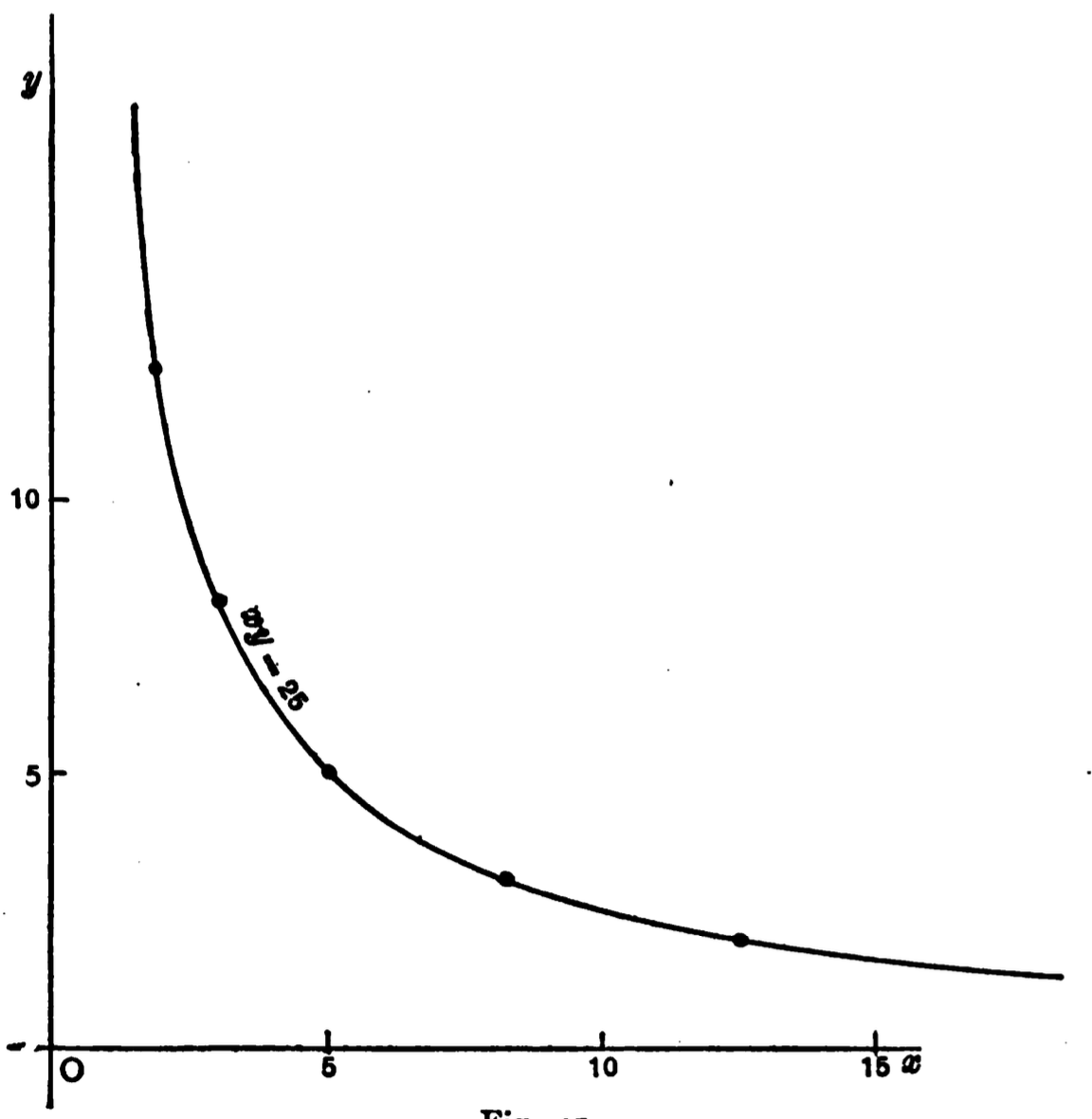


Fig. 32
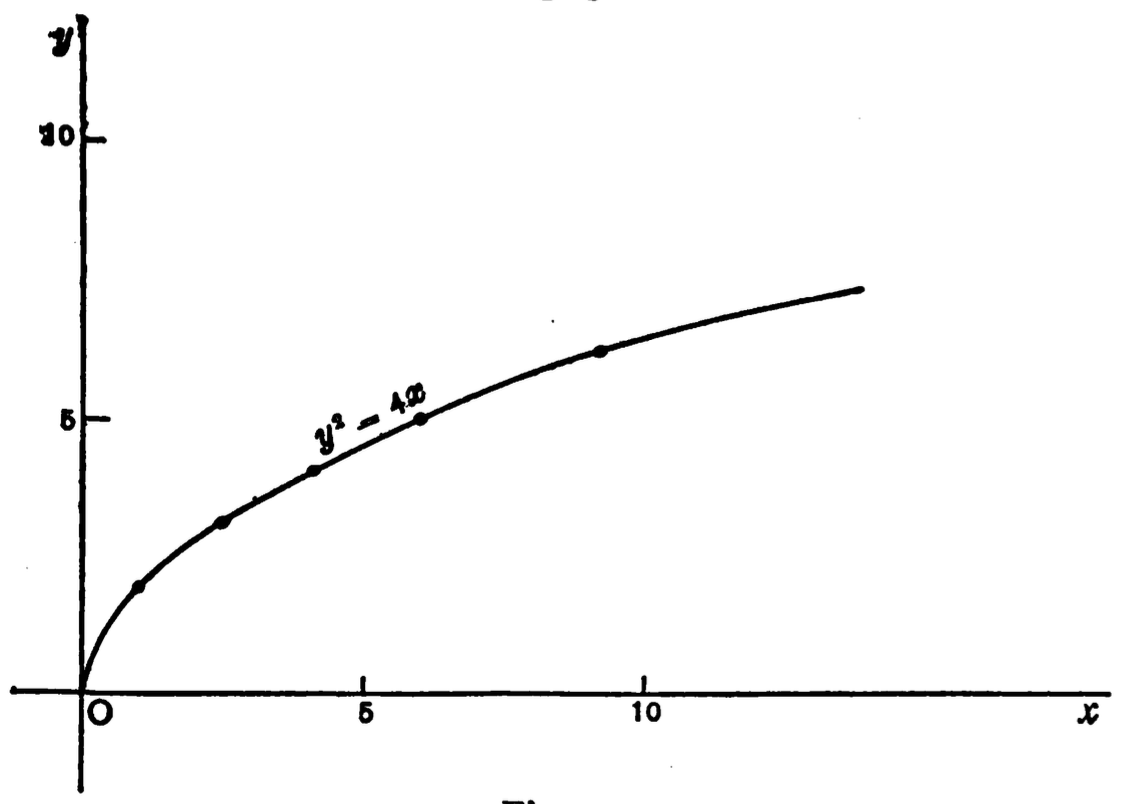


Fig. 33
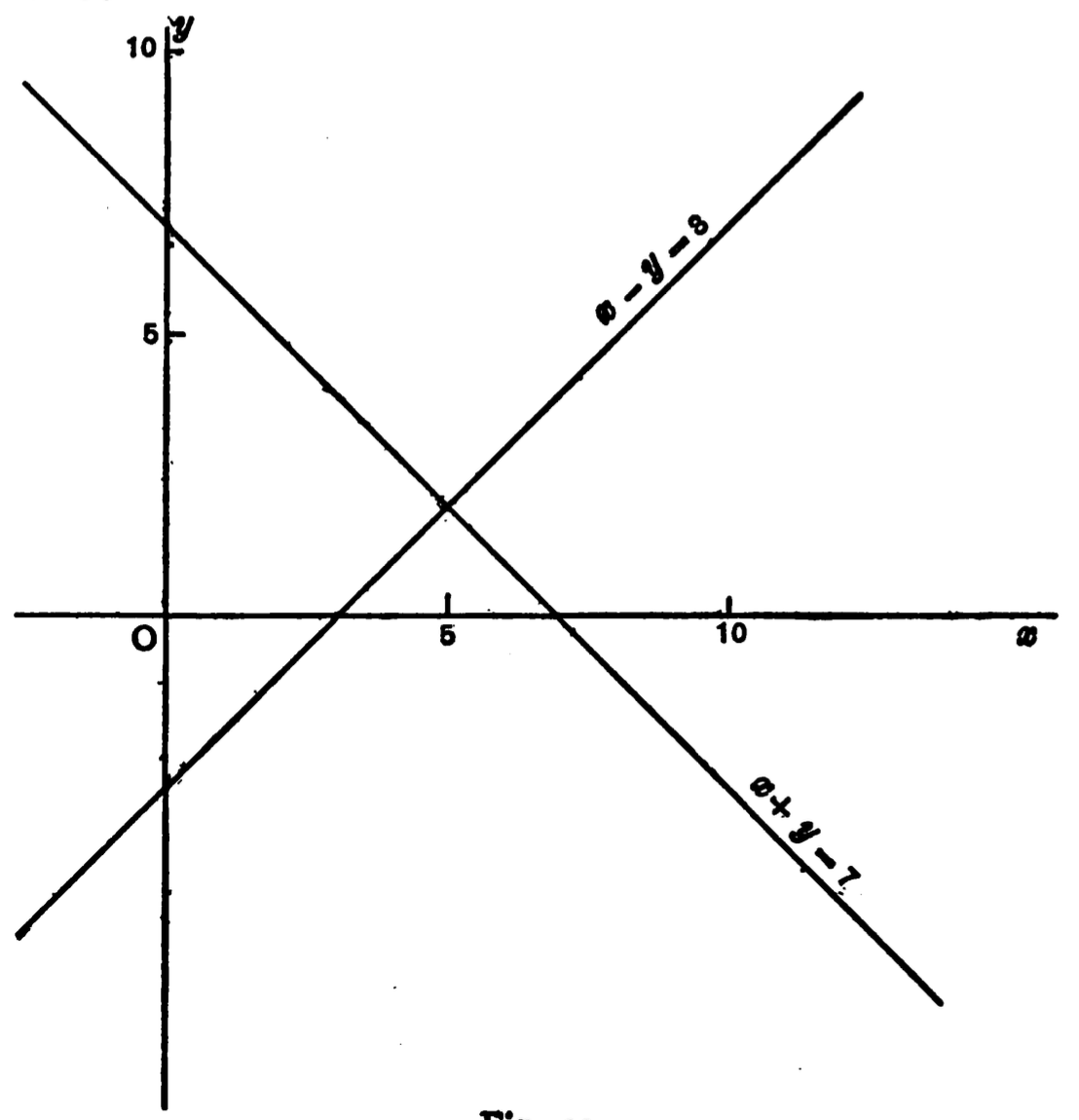


Fig. 34


Fig. 35



Fig. 36
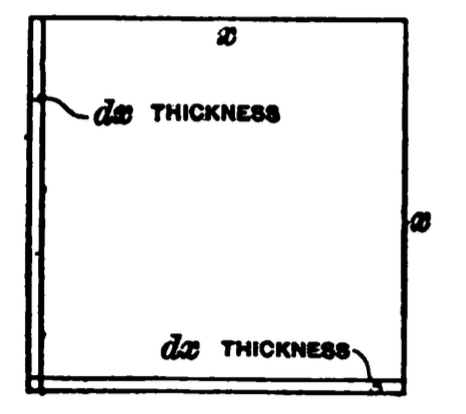


Fig. 37
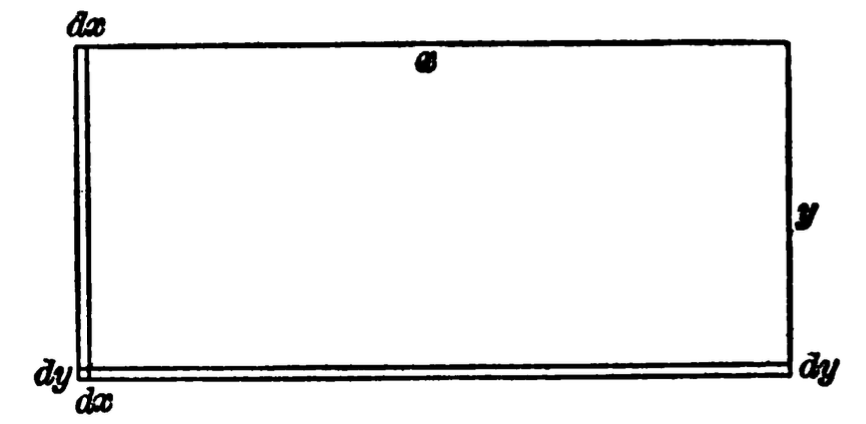


Fig. 38
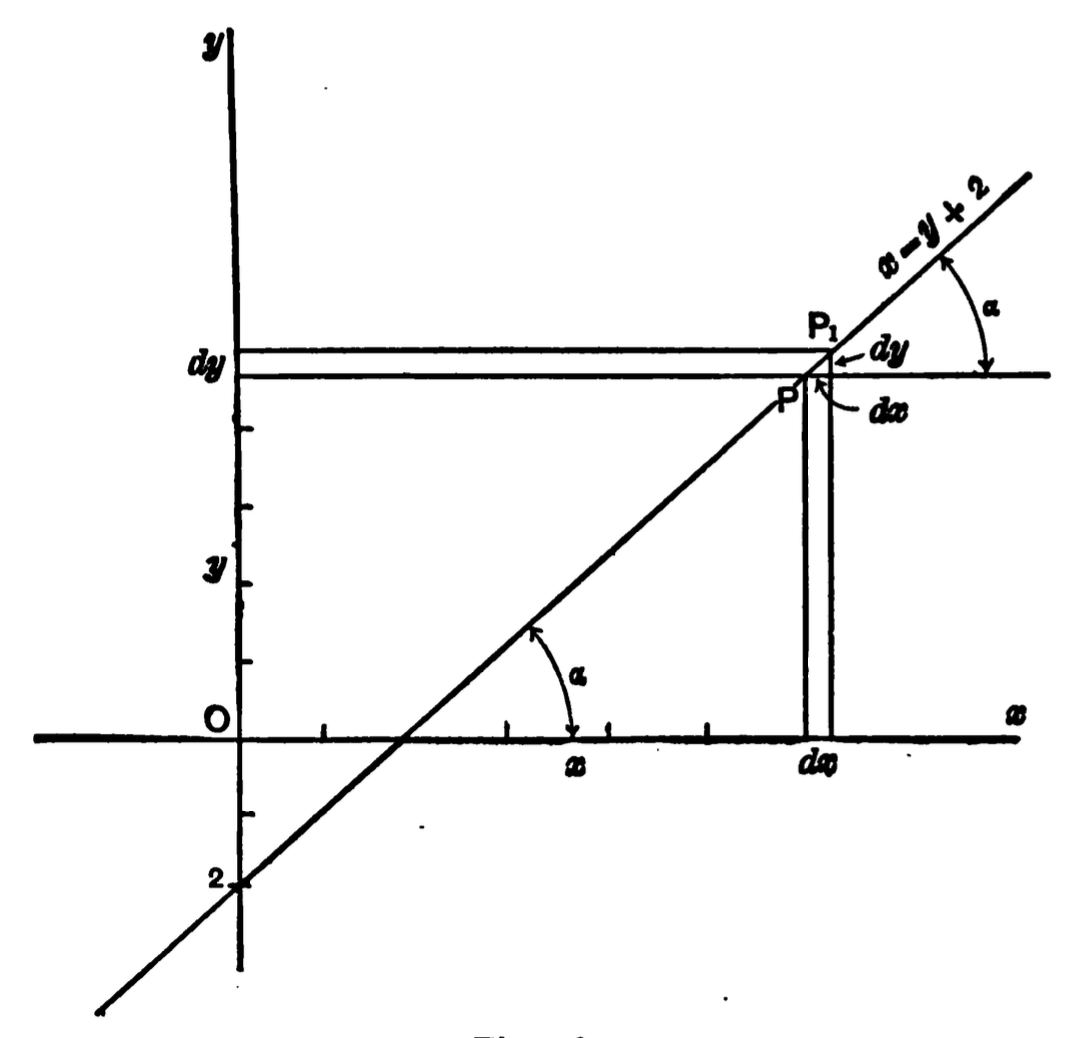


Fig. 39
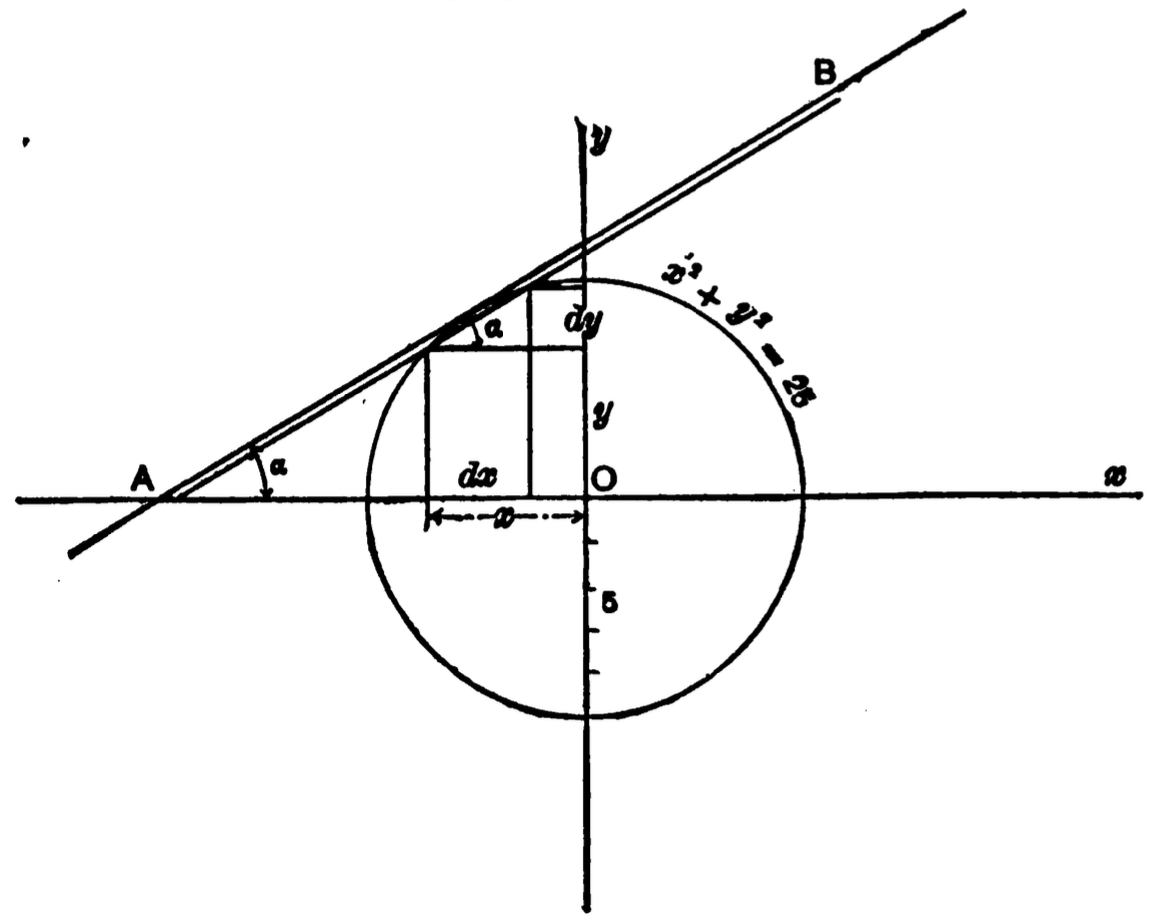


Fig. 40
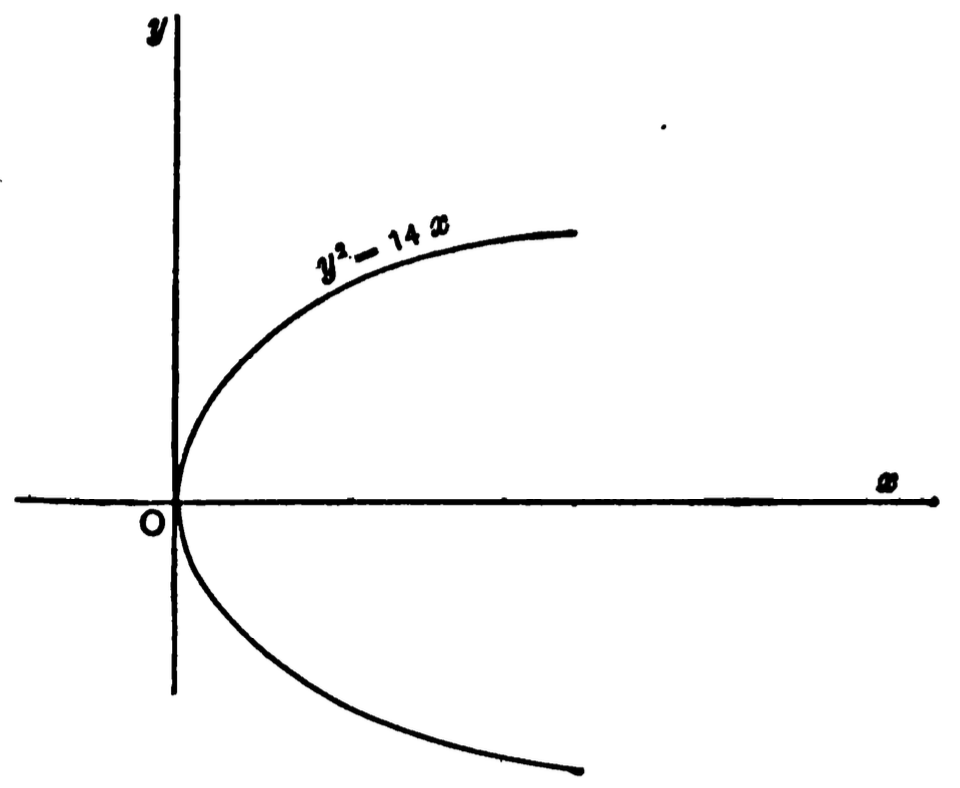


Fig. 41
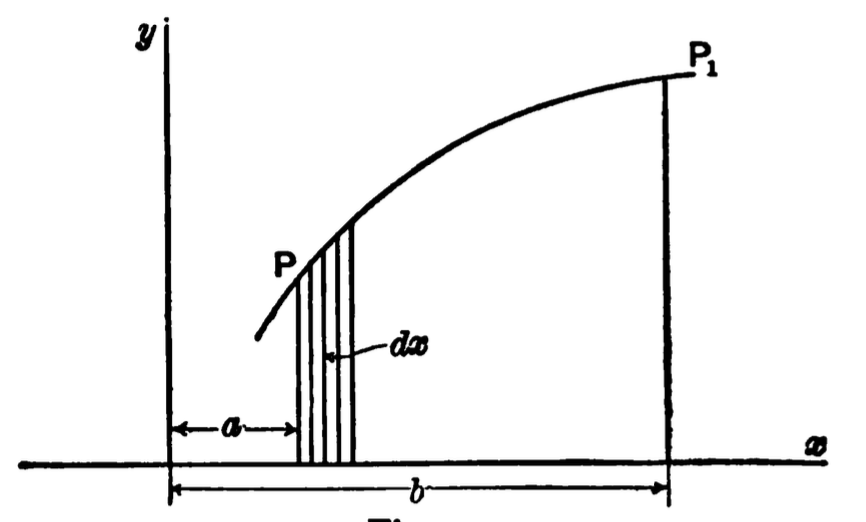


Fig. 42